Komplexaufgaben
Aufgabe
Kapitel 3
Die Kreiszahl \(\pi\) kann mit Hilfe der folgenden Summenformel approximiert werden.
Schreiben Sie zwei Funktionen mit dem Eingangsparameter \(N\), die \(\pi\) approximieren.
- Verwenden Sie eine
for-Schleife für die Approximation von \(\pi\).
Ermitteln Sie die durchschnittliche Laufzeit des Programms. - Verwenden Sie die
sum-Funktion. Vergleichen Sie die Laufzeit.
Lösung
function [result] = Pi1(N)
summe = 0;
for n = 0:N
summe = summe + (-1)^n * 1/(2*n+1);
end
result = summe * 4;
end
>> tic;Pi1(1e8),toc
ans =
3.141592663589326
Elapsed time is 2.463820 seconds.
function [result] = Pi2(N)
n = 0:N;
result = 4*sum((-1).^n * 1./(2*n+1));
end
>> tic;Pi2(1e8),toc
ans =
3.141592663590250
Elapsed time is 1.545192 seconds.
Aufgabe
Kapitel 3
Approximieren Sie die Kreiszahl \(\pi\) mit dem Monte-Carlo-Algorithmus:
- Es werden zufällig \(N\) Punkte \(P(x, y)\) aus dem Quadrat \(0 \leq x \leq 1,\quad 0 \leq y \leq 1\) ausgewählt. Tipp:
rand-Funktion verwenden! - Mit der Bedingung \(x^2 + y^2 \leq 1\) wird die Anzahl \(N_K\) der Punkte bestimmt, die sich innerhalb des Einheitskreises befinden.
-
Es ist anzunehmen, dass die Größe der Fläche proportional zur Anzahl der Punkte innerhalb dieser Fläche ist. Es gilt:
\[ \frac{\text{Viertelkreisfläche}}{\text{Quadratfläche}} = \frac{\pi}{4} \approx \frac{N_K}{N} \]
-
\(\pi\) wird approximiert durch:
\[ \pi \approx 4 \cdot \frac{N_K}{N} \]
Schreiben Sie eine Funktion, die \(\pi\) mit Hilfe des Monte-Carlo-Algorithmus approximiert. Diese Funktion hat \(N\) als Eingabeparameter.
Vergleiche Sie Laufzeit und Genauigkeit mit den vorangegangen Funktionen.
Kapitel 5
Stellen Sie die Funktionsweise des Monte-Carlo-Algorithmus graphisch dar, indem Sie die folgende Abbildung generieren.
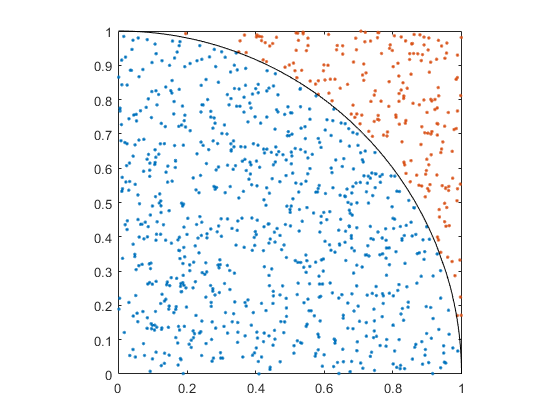
Lösung
function [result] = Pi3(N)
Nk = 0;
for n = 1:N
x = rand;
y = rand;
if x^2 + y^2 <= 1
Nk = Nk + 1;
end
end
result = 4 * Nk / N;
end
>> tic;Pi3(1e8),toc
ans =
3.141816720000000
Elapsed time is 8.017909 seconds.
N = 1000;
in = [];
out = [];
Nk = 0;
for n = 1:N
x = rand();
y = rand();
if x^2 + y^2 <= 1
Nk = Nk + 1;
in = [in, [x; y]];
else
out = [out, [x; y]];
end
end
result = 4 * Nk / N
clear x y
plot(in(1,:), in(2,:), '.')
hold('on');
plot(out(1,:), out(2,:), '.')
axis('equal')
fplot(@(x) sqrt(1-x.^2), [0 1], 'k')
xlim([0, 1]);ylim([0, 1]);
hold('off');
Aufgabe
Kapitel 3
-
Pythagoreische Tripel sind drei ganzzahlige Seitenlängen, die ein rechtwickliges Dreieck bilden:
\[ (a, b, c)^T \in \mathbb N^3 | a^2 + b^2 = c^2 \]Beispiel: Das kleinste pythagoreische Tripel: \((3, 4, 5)\), da $ 3^2 + 4^2 = 25 = 5^2$
- Schreiben Sie ein Skript, dass alle pythagorischen Tripel für \(a, b < N\) findet und in einer Matrix ausgibt.
Kapitel 5
- Stellen Sie die Verteilung der pythagoreischen Tripel graphisch dar. Markieren Sie den Punkt \(P(a, b)\) im Graphen, der einem pythagoreischen Tripel entspricht.
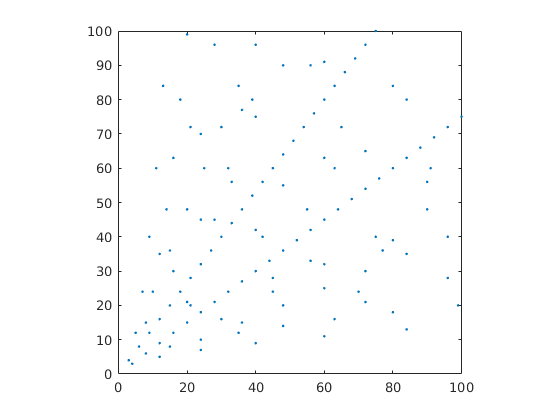
- Kann das Programm optimiert werden, wenn die Reihenfolge der Tripel in der Ausgabe nicht relevant ist?
Lösung
N = 100
tripel = [];
for a = 3:N
for b = (a + 1): N
c = sqrt(a^2 + b^2);
if floor(c) == c
tripel = [tripel; [a, b, c]];
tripel = [tripel; [b, a, c]];
end
end
end
tripel
plot(tripel(:,1), tripel(:,2), '.');
axis('square')
- Es gibt keine Tripel mit \(a, b < 3\).
- Es gibt keine Tripel für \(a = b\).
- Ist \((a, b, c)\) ein Tripel, so ist auch \((b, a, c)\) ein Tripel.
Aufgabe
Kapitel 3
Schreiben Sie ein Programm, das ein Polynom \(f(x)\) n-ten Grades aus verschiedenen Bedingungen berechnet.
Die Bedingungen haben die folgende Form:
Schauen Sie sich die folgenden Lösung für ein Menü an:
Lösung
Beispielfunktion:

Lösung:
N = input('Grad der Funktion: ')
K = zeros(N + 1);
Y = zeros(N + 1, 1);
for m = 1:(N+1)
fprintf('%d. Bedingung:\n', m);
fprintf(' 1) y = f(x)\n');
fprintf(' 2) s = f''(x)\n');
fprintf(' 3) c = f''''(x)\n');
type = input('>> ');
x = input('x = ');
switch type
case 1
y = input('y = ');
for n = 0:N
K(m, n+1) = x^n;
end
Y(m) = y;
case 2
s = input('s = ');
for n = 1:N
K(m, n+1) = n * x^(n-1);
end
Y(m) = s;
case 3
y = input('c = ');
for n = 2:N
K(m, n+1) = n * (n-1) * x^(n-2);
end
Y(m) = c;
end
end
A = K\Y;
A'
Aufgabe
Kapitel 4
Schreiben Sie ein Skript, dass die Tangente einer beliebigen Funktion \(f(x)\) im Punkt \(x_t\) berechnet.
Stellen Sie die Funktion f und die Tangentenfunktion ft graphisch mit den folgenden Befehlen dar:
Lösung
Aufgabe
Kapitel 4
Programmieren Sie ein Skript, dass automatisch eine Kurven-Diskussion durchführt. Das Skript soll alle Nullstellen, Minima, Maxima und Wendepunkte einer reellen Funktion angeben.
Beispiel:
Lösung
syms x
f(x) = x^3-2*x + 2
x_ns = solve(f == 0, x);
if ~ isempty(x_ns)
for x_n = unique(x_ns)'
fprintf('Nullstelle: x_n = %d\n', x_n);
end
end
fdx = diff(f, x);
fddx = diff(fdx, x);
x_es = solve(fdx == 0, x);
if ~ isempty(x_es)
for x_e = unique(x_es)'
y_e = f(x_e);
c_e = fddx(x_e);
if c_e > 0
fprintf('Minimum: T(%d, %d)\n', x_e, y_e);
elseif c_e < 0
fprintf('Maximum: H(%d, %d)\n', x_e, y_e);
else
fprintf('Sattelpunkt: S(%d, %d)\n', x_e, y_e);
end
end
end
x_ws = solve(fddx == 0, x);
if ~ isempty(x_ws)
for x_w = unique(x_ws)'
y_w = f(x_w);
fprintf('Wendepunkt: W(%d, %d)\n', x_w, y_w);
end
end
Aufgabe
Kapitel 4
Simulieren Sie die Bewegung einer einfeldriger Brücke mit konzentrierter Eigenlast in der Mitte anhand der Bewegungsgleichung.
Als Anfangsbedingungen sollen eine 1cm Auslenkung und keine Anfangsgeschwindigkeit angenommen werden.
Folgende Werte sind zu definieren:
- \(y(t)\): die Position des Diskretisierungspunktes
- \(m\): die Masse der Konstruktion
- \(d\): die Dämpfung (Luftwiderstand und Reibung)
- \(k\): die Steifigkeit der Feder (Konstruktion)
Zunächst ist die Lösung der Differentialgleichung zu finden und anschließend folgende Werte einzusetzen:
- \(m = 20000\,\text{kg}\)
- \(d = 500 \,\text N/\text s\)
- \(k = 10000 \,\text N/ \text m\)
Schließlich soll die Lösung dargestellt werden