Skip to content

Plots

Darstellen von 2D-Graphen

  • Verwenden von fplot für das einfache Darstellen von Funktionen:
    >> fplot(@(x) sin(x))
  • Einstellen des Intervalls der x-Werte:
    >> fplot(@(x) sin(x), [0, 2*pi])

    → y-Bereich wird automatisch bestimmt aus minimalem und maximalem Funktionswert.

Funktionen zum Anpassen und Beschriften von Abbildungen

  • title(text): Titel über dem Graphen.
  • xlabel(text), ylabel(text): Beschriftung der x- und y-Achse.
  • xlim([min, max]), ylim([min, max]): Intervall der x- und y-Achse.
  • xticks([...]), yticks([...]): Zahlen an der x- und y-Achse.
  • grid('on'), grid('off'): Gitter aktivieren oder deaktivieren.
  • legend({'Graph1', 'Graph2'}): Legenden bei der Anzeige mehrere Graphen in einer Abbildung.

Aufgabe

Stellen Sie die ersten beiden Perioden der Sinusspannung \(u(t) = \sqrt 2\cdot 230\,\text V \cdot \sin\left(2\pi\cdot 50\,\text{Hz}\cdot t\right)\) graphisch dar. Beschriften Sie den Graph, wie im folgenden Bild.

w:50

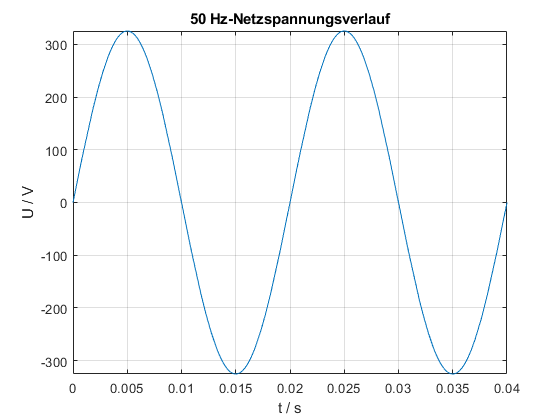
Lösung

fplot(@(t) 230 * sqrt(2) * sin(2*pi*50*t), [0, 2/50])
xlabel('t / s')
ylabel('U / V')
title('50 Hz-Netzspannungsverlauf')
grid('on')

Beispiel

Verwenden Sie den hold('on')-Befehl, um eine Sinus- und eine Cosinus-Schwingung in einer Abbildung gleichzeitig darzustellen.

fplot(@(t) 230 * sqrt(2) * sin(2*pi*50*t), [0 1/25])
hold('on')
fplot(@(t) 230 * sqrt(2) * cos(2*pi*50*t), [0 1/25])
legend('Sinus-Schwingung', 'Cosinus-Schwingung')
hold('off')

→ Wenn der hold('on')-Befehl in einem Skript verwendet wird, sollte ein hold('off')-Befehl am Ende des Skriptes folgen, um den Ausgangszustand wiederherzustellen. Sonst kann es passieren, dass weitere Graphen in diesen Plot gezeichnet werden.

Aufgabe

Zeichnen Sie die drei Außenleiterspannungen eines Dreiphasenwechselstrom-Systems. Die Amplitude der Spannungen beträgt \(\widehat u = \sqrt 2 \cdot 230\,\text V\), die Frequenz beträgt \(50\,\text{Hz}\) und die Phasen sind um jeweils \(-120^\circ\) verschoben.

Erzeugen Sie die folgende Abbildung :
w:50

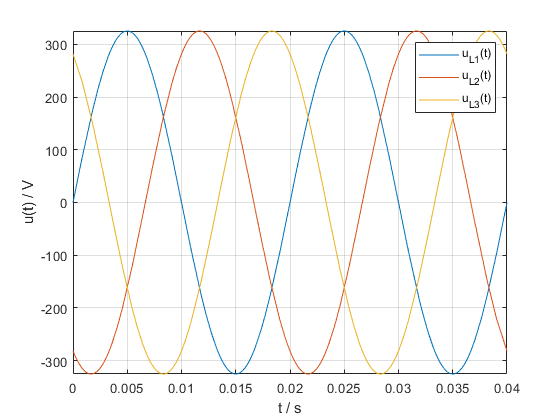
Lösung

fplot(@(t) 230 * sqrt(2) * sin(2*pi*50*t), [0 1/25])
hold('on')
fplot(@(t) 230 * sqrt(2) * sin(2*pi*50*t - 2*pi/3), [0 1/25])
fplot(@(t) 230 * sqrt(2) * sin(2*pi*50*t + 2*pi/3), [0 1/25])
xlabel('t / s')
ylabel('u(t) / V')
legend('u_{L1}(t)', 'u_{L2}(t)', 'u_{L3}(t)')
grid('on')
hold('off')

Anpassen der Farbe, Marker und Linietyp der Graphen

siehe https://de.mathworks.com/help/matlab/ref/linespec.html

w:50

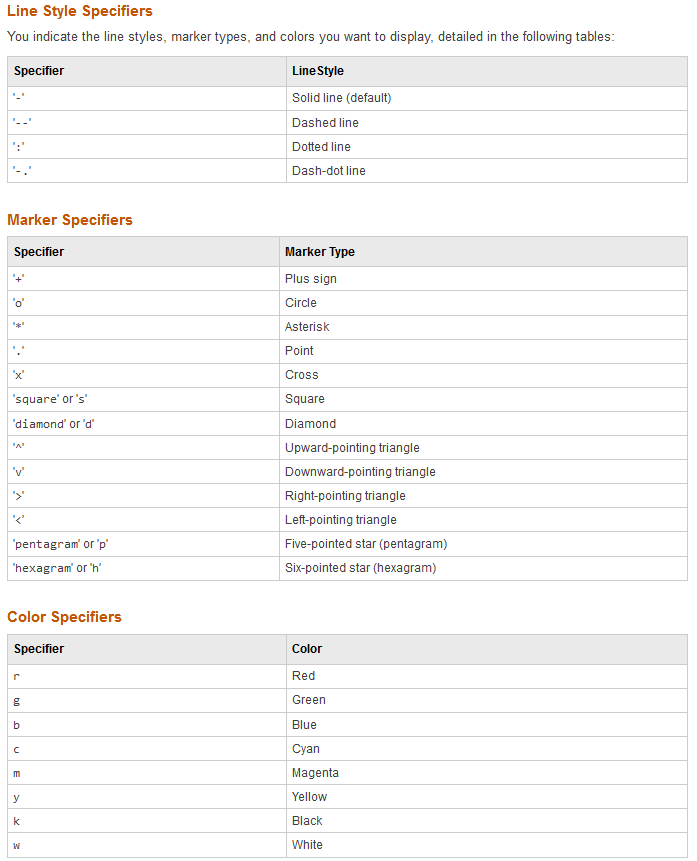
Beispiel:

fplot(@(t) 230 * sqrt(2) * sin(2*pi*50*t), [0 1/25], '--xr')

Abspeichern der Figure

  • Der Graph kann über File → Save abgespeichert werden.
  • Es stehen mehrere Ausgabeformate zur Verfügung:
    • .fig - MATLAB-Figure:
      Internes MATLAB-Format. Eine Figure-Datei kann wieder mit MATLAB geöffnet werden. Der Graph kann bearbeitet werden. (Kleine Fehler können ausgebessert werden). .fig-Dateien können in der Regel nicht in andere Programme importiert werden.
    • .png, .bmp: Verlustfreie Rastergrafiken
      Für den Export des Figures in eine Webseite. Das Bild besitzt in der Regel eine geringe Auflösung.
    • .svg, .eps, .pdf, .emf: Vektorgrafiken
      Zum Einfügen des Figures in LaTeX oder Word. Vektorgrafiken können beliebig skaliert werden. Aus diesem Grund entstehen keine Skalierungsartefakte. .emf für neue Versionen für Word

Beispiel

Verwenden Sie den subplot-Befehl, um mehrere Graphen in einer Abbildung nebeneinander anzuzeigen.

Verwenden der subplot(m, n, p)-Funktion
→ Erstellen eines \(m\times n\)-Rasters (\(m\): Zeilen, \(n\): Spalten)
Der nächste Graph wird in die Position \(p\) gezeichnet. Es wird zuerst spaltenweise nummeriert.

Lösung

Beispiel:
w: 75

subplot(2, 1, 1)
fplot(@(t) 230 * sqrt(2) * sin(2*pi*50*t), [0 1/25])
subplot(2, 1, 2)
fplot(@(t) 230 * sqrt(2) * cos(2*pi*50*t), [0 1/25])

Es können für p auch mehrere Elemente angegeben werden. So können Graphen in unterschiedlichen Größen ausgegeben werden.

subplot(2, 2, [1,3])
fplot(@(t) 230 * sqrt(2) * sin(2*pi*50*t), [0 1/25])
subplot(2, 2, 2)
fplot(@(t) 230 * sqrt(2) * cos(2*pi*50*t), [0 1/25])
subplot(2, 2, 4)
fplot(@(t) 230 * sqrt(2) * tan(2*pi*50*t), [0 1/25])

Aufgabe

Schreiben Sie das vorangegange Skript um, damit die Graphen nebeneinander dargestellt werden.

Lösung

Verwenden des subplot-Befehls für mehrere Graphen verschiedener Größen.

subplot(3,4,[1 2 5 6]);
subplot(3,4,[3 4 7 8]);

Verwenden des Plot-Befehls

Mit Hilfe des Plot-Befehls können eine Vielzahl von Graphen dargestellt werden. Dieser Befehl stellt Punkte auf einem Graphen dar und verbindet diese.

Beispiel

Stellen Sie die Folge \({3, 6, 1, 2, 5}\) graphisch dar.

x = [1 2 3 4 5];
y = [3 6 1 2 5];

plot(x, y)

Schauen Sie sich die Ausgabe des folgenden Skriptes an. Interpretieren Sie das Ergebnis.

x = [1 2 3 4 5 0];
y = [3 6 1 2 5 0];

plot(x, y)

Beispiel

Stellen Sie die 50-Hz-Sinusschwingung mit Hilfe des plot-Befehls dar.

t = linspace(0, 1/25, 100);
u = sqrt(2)*230*sin(2*pi*50*t);

plot(t, u)
  • Ein Zeitvektor wird mit Hilfe der linspace-Funktion erzeugt. 100 Werte werden von 0 bis 1/25 gleich verteilt.
  • Es werden elementweise die Spannungswerte berechnet.
  • Beide Vektoren werden zum Zeichnen des Plots übergeben.

Aufgabe

Stellen Sie die Kondensator-Ladefunktion mit Hilfe der plot-Funktion graphisch dar.

\[ u_C(t) = U_q\cdot \left( 1 - e^{-\frac{t}{R\cdot C}} \right) \]
\[ R = 1\,\text k\Omega, \quad C = 4{,}7\,\mu\text F, \quad U_q = 5\,\text V\]

Lösung

Welche Zeitbasis?

\[ \tau = R \cdot C = 4{,}7\,\text{ms} \rightarrow t_{max} = 5 \tau \approx 25\,\text{ms}\]
% Berechnung der Kondensatorspannung beim Aufladevorgang

%% Eingangsgrößen
R = 1e3;     % in Ohm
C = 4.7e-6;    % in F
Uq = 5;        % in V
t_max = 25e-3; % in sec

%% Berechnung
t = linspace(0, t_max, 100);

tau = R*C;
uc = Uq * (1 - exp(-t/tau));

%% Plot
plot(t*1e3, uc)
xlabel('t / ms')
ylabel('u_C / V')

Aufgabe

Stellen Sie den Einheitskreis mit Hilfe einer Parameterfunktion und dem plot-Befehl graphisch dar.

\[ x = \cos t \]
\[ y = \sin t \]
\[ t \in [0, 2\pi] \]

Lösung

%Einheitskreis plot

%% Berechnung
t=linspace(0,2*pi,100);
x=cos(t);
y=sin(t);

%% Plot
plot(x,y)
%axis('equal')
axis('square')
  • Ohne Axis-Square wird der Plot als Ellipse dargestellt
  • Verwenden von axis('square') oder axis('equal'), um die x- und y-Achse gleich einzuteilen.

Darstellen von Polarplots

Beispiel

Stellen Sie die folgende Polarfunktion graphisch dar.

\[r(\varphi) = \sin(2\varphi) \cdot \cos(2\varphi)\]

mit

\[\varphi \in [0, 2\pi]\]

  1. Möglichkeit: Umwandeln der Polarkoordinaten in kartesische Koordinaten

    \[ x = r(\varphi)\cdot \cos \varphi, \quad y = r(\varphi)\cdot \sin \varphi\]
    phi = linspace(0, 2*pi, 500);
r = sin(2*phi) .* cos(2*phi);

x = r .* cos(phi);
y = r .* sin(phi);

plot(x, y);
axis('square')

  2. Möglichkeit: Verwendung des polarplot-Befehls

    phi = linspace(0, 2*pi, 500);
r = sin(2*phi) .* cos(2*phi);

polarplot(phi, r);

Aufgabe

Stellen Sie die Richtwirkung von Antennen graphisch dar.

In der Hochfrequenztechnik wird die Antennenlänge \(l\) in Abhängigkeit der Wellenlänge \(\lambda\) der Trägerfrequenz \(f\) angegeben.

Der Zusammenhang zwischen Wellenlänge und Trägerfrequenz: \(\lambda = \frac{c}{f}\).

Normieren Sie die Darstellung, indem Sie die Graphen für \(E_0 = 1\) zeichnen.

  • \(l = \lambda / 2\) (Halbwellenstab):

    \[ E(\vartheta) = E_0 \cdot\left| \frac{\cos\left( \frac{\pi}{2} \cos \vartheta \right)}{\sin \vartheta}\right| \]

  • \(l = 1\cdot\lambda\) (Vollwellenstab)

    \[ E(\vartheta) = E_0 \cdot\left| \frac{\sin\left( \pi \cos \vartheta \right)}{\sin \vartheta}\right| \]

  • \(l = \frac{3}{2} \lambda\)

    \[ E(\vartheta) = E_0 \cdot\left| \frac{\cos\left( \frac{3\pi}{2} \cos \vartheta \right)}{\sin \vartheta}\right| \]

Lösung

theta = linspace(1e-5, 2*pi-1e-5, 200);
E1 = abs(cos(pi/2*cos(theta)) ./ sin(theta));
E2 = abs(sin(pi*cos(theta)) ./ sin(theta));
E3 = abs(cos(3*pi/2*cos(theta)) ./ sin(theta));

polarplot(theta, E1);
hold('on')
polarplot(theta, E2);
polarplot(theta, E3);
hold('off')

Die Graphen haben bei \(\vartheta = k\cdot 2\pi\) eine Unstetigkeit. Um diese zu kaschieren, werden diese Werte ausgeklammert.

Lösung

Setzen von weiteren Einstellungen des Polarplots:

pax = polaraxes;
polarplot(pax, phi, r);
pax.ThetaDir = 'clockwise';
pax.ThetaZeroLocation = 'bottom';
thetalim([0 180]);

Der polarplot-Befehl kann auch für die Darstellung komplexer Funktionen verwendet werden!

3D-Plots

  • MATLAB besitzt eine Vielzahl von Befehlen für die grafische Darstellung dreidimensionaler Funktionen.
  • Es muss im Dreidimensionalen zwischen der Darstellung von Kurven und Flächen unterschieden werden.

Darstellung von 3D-Kurven

Die Darstellungen von Kurven im Dreidimensionalen erfolgt häufig in der Parameter-Form. Bei einer Kurve gibt es immer einen freien Parameter.

Beispiel

Stellen Sie die folgende dreidimensionale Kurve mit Hilfe der plot3-Funktion graphisch dar.

\[ x = \cos t \]
\[ y = \sin t \]
\[ z = t \]
\[ t \in [0, 10\pi] \]
t = linspace(0, 10*pi, 500);

x = cos(t);
y = sin(t);
z = t;

plot3(x, y, z);

Stellen Sie die Kurve mit Hilfe der axis('equal')-Funktion maßstabsgetreu dar. Wie muss die Funktion verändert werden, um die Feder wieder zusammenzudrücken?

Lösung

z = t/10;

Aufgabe

Stellen Sie die folgende Funktion graphisch dar.

\[ x = t \cdot \cos t \]
\[ y = t \cdot \sin t \]
\[ z = t \]
\[ t \in [0, 5\pi] \]

Lösung

t = linspace(0, 5*pi, 500);

x = t.*cos(2*t);
y = t.*sin(2*t);
z = t;

plot3(x, y, z);
axis equal

Aufgabe

Stellen Sie die folgende Funktion graphisch dar.

\[ x = \sin t \cdot \cos(20t) \]
\[ y = \sin t \cdot \sin(20t) \]
\[ z = \cos t \]
\[ t \in [0, \pi] \]

Lösung

t = linspace(0, pi, 500);

x = sin(t).*cos(20*t);
y = sin(t).*sin(20*t);
z = cos(t);

plot3(x, y, z);
axis equal

Darstellen von 3D-Flächen

  • Flächen im Dreidimensionalen haben immer zwei freie Parameter.

  • Oft werden Flächen als Graph über der x-y-Ebene dargestellt (Höhenkarte):

    \[ z = f(x, y) \]

Beispiel

Stellen Sie die folgende Fläche graphisch dar.

\[ z = f(x, y) = \sin\left( \sqrt{x^2 + y^2} \right)\]
\[ (x, y)^T \in [-5, 5] \times [-5, 5] \]
[x, y] = meshgrid(linspace(-5, 5, 50), linspace(-5, 5, 50));
z = sin(sqrt(x.^2 + y.^2));

surf(x, y, z);

Erklärung zur meshgrid-Funktion

  • In der Regel wird in MATLAB die meshgrid-Funktion verwendet, um die Matrizen der freien Parameter zu erstellen, mit denen elementweise die Koordinaten eines Punktes der Fläche berechnet werden können.
  • Eingabeparameter: Verteilung der freien Parameter als Vektor.
  • hier: Verwendung der linspace-Funktion, um Werte aus \([-5, 5]\) zu erhalten.
  • Ausgabewert: x- und y-Matrix, sodass elementweise die z-Koordinate aller x- und y-Kombinationen berechnet werden können.
  • Vereinfachtes Beispiel:
    >> [x, y] = meshgrid([1, 2, 3], [4, 5, 6])
x =
    1     2     3
    1     2     3
    1     2     3
y =
    4     4     4
    5     5     5
    6     6     6
>> 10*x + y
ans =
    14    24    34
    15    25    35
    16    26    36

Funktionen zur Darstellung von 3D-Flächen

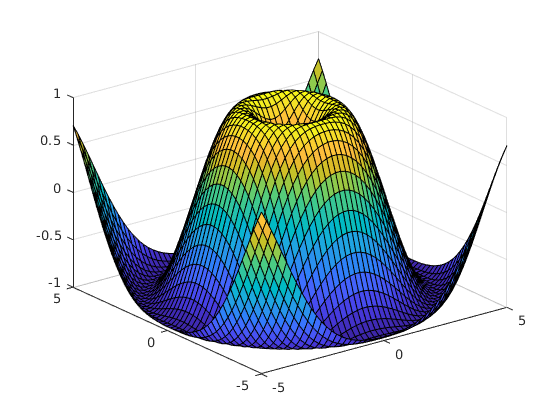
  • surf-Funktion
    Darstellung der Fläche als 3D-Oberfläche
    w: 33
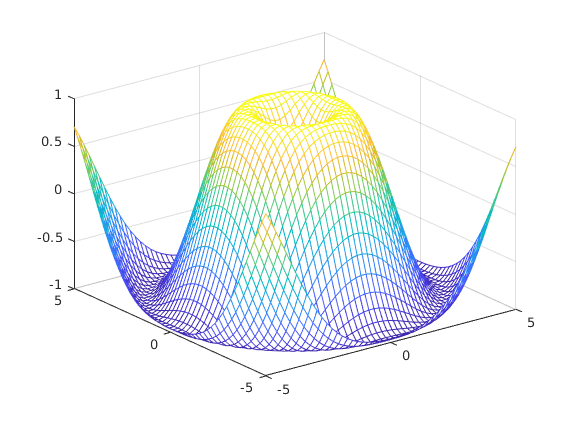
  • mesh-Funktion
    Darstellung der Fläche als Maschennetz
    w: 33
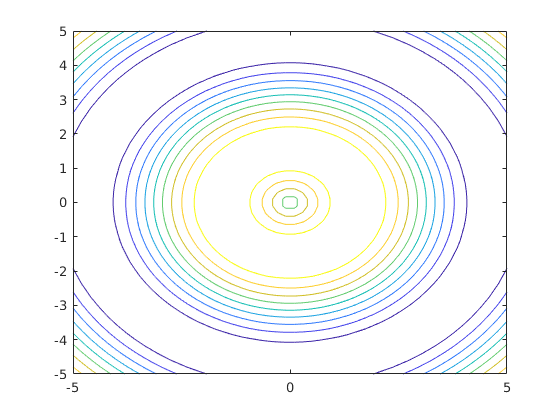
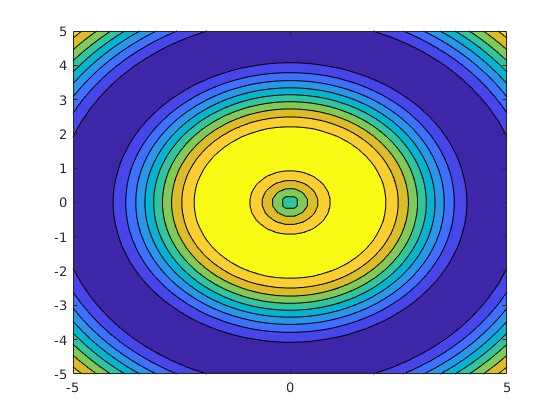
  • contour und contourf
    Höhenkarte des Graphen in 2D
    w: 33 w: 33

Aufgabe

Stellen Sie die folgende Wellenfunktion graphisch dar.

\[ z = f(x, y) = \sin x \cdot \sin y \]

Lösung

[x, y] = meshgrid(linspace(-2*pi, 2*pi, 100), linspace(-2*pi, 2*pi, 100));
z = sin(x) .* sin(y);

Aufgabe

Die Lösung einer partiellen Differentialgleichung ergibt die folgende Wärmeleitgleichung im Intervall \((x, y) \in [0, \pi] \times [0, 5]\).

Stellen Sie eine Approximation der Lösung graphisch dar.

\[ T(x, y) = \sum_{n=0}^{\infty} \frac{4}{(2n+1)\pi} \sin\left( (2n+1)\,x \right)e^{-(2n+1)\,y} \]

Tipp:
Schreiben Sie die ersten vier Glieder der Funktion aus. Stellen Sie die Summe der ersten vier Glieder graphisch dar. Versuchen Sie anschließend die Summe von \(n\) Gliedern mit einer for-Schleife zu berechnen.

Zusatz:
Wie kann die Funktion verändert werden, sodass \(T_1 = 20^\circ C\) und \(T_2 = 50^\circ C\) gilt?

Lösung

Skizze der Wärmeverteilung am Rand der betrachteten Fläche.

Partielle Differentialgleichung:

\[ \Delta u(x,y) = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0\]

Randwerte:
w: 50

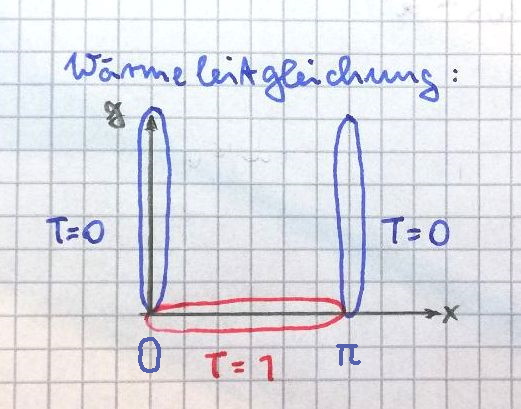
Lösung

[x, y] = meshgrid(linspace(0, pi, 100), linspace(0, 5, 100));
z = 4 / (1*pi) * sin(1*x) .* exp(-1*y) ...
    + 4 / (3*pi) * sin(3*x) .* exp(-3*y) ...
    + 4 / (5*pi) * sin(5*x) .* exp(-5*y) ...
    + 4 / (7*pi) * sin(7*x) .* exp(-7*y);

Verwenden einer for-Schleife:

[x, y] = meshgrid(linspace(0, pi, 100), linspace(0, 5, 100));
z = 0;
for n = 0:100
    z = z + 4 / ((2*n+1)*pi) * sin((2*n+1)*x) .* exp(-(2*n+1)*y);
end

Zusatz:
Es handelt sich um eine lineare partielle Differentialgleichung, also gilt:

\[ \widetilde T (x, y) = (20 + 30 \cdot T(x, y)) \,^\circ C \]

Aufgabe

Stellen Sie die Oberfläche einer Kugel graphisch dar.

Tipp:
Eine Kugeloberfläche kann nicht als Graph dargestellt werden. Verwenden Sie die Polardarstellung der Kugel und \(\varphi, \vartheta\) als die beiden freien Parameter.

Lösung

\[ F(\varphi, \vartheta) = \begin{pmatrix} \sin \vartheta \cos \varphi \\ \sin \vartheta \sin \varphi \\ \cos \vartheta \end{pmatrix}\]

mit

\[\vartheta \in [0, \pi], \quad \varphi \in [0, 2\pi]\]
[theta, phi] = meshgrid(linspace(0, pi, 19), linspace(0, 2*pi, 37));
x = sin(theta) .* cos(phi);
y = sin(theta) .* sin(phi);
z = cos(theta);

surf(x, y, z);
axis('equal')