Messreihen

Überblick:

• Möglichkeiten Messreihen einzulesen.
• Kurz: Darstellung von Messreihen in Plots.
• Möglichkeiten der Auswertung von Messreihen:
  • Regression.
  • Berechnung der Fläche unter der Kurve.
  • Kurvendiskussion mit Polynomen.

Einlesen von Messreihen in MATLAB

Darstellen in einer .m-Datei

Beispiel

Übertragen Sie die folgende Messreihe in ein MATLAB-Skript:

\(U_B/\text V\)	0	0.5	1	1.5	2	2.5	3	3.5	4
\(I_B/\text{mA}\)	0	40	70	100	122	144	158	165	170

---

1. Möglichkeit: Aufschreiben als zwei Vektoren.
   

   u_b = [0,.5,1,1.5,2,2.5,3,3.5,4];
   i_b = [0,40,70,100,122,144,158,165,170] .* 1e-3;
   

2. Möglichkeit: Aufschreiben einer Datenmatrix.
   

   data = [0 0
         .5 40
         1 70
         1.5 100
         2 122
         2.5 144
         3 158
         3.5 165
         4 170];
   u_b = data(:,1)';
   i_b = data(:,2) .* 1e-3';
   

Datenimport aus Excel-Dokumenten

Beispiel

Download: daten1.csv

Laden Sie die Tabelle in das MATLAB-Workspace. Verwenden Sie die csvread-Funktion, um die Daten in MATLAB einzulesen. Erstellen Sie wie im vorangegangen Beispiel die Vektoren u_b und i_b, die die Werte in SI-Grundeinheiten enthalten.

---

Beim Einlesen der csv-Datei muss die erste Zeile übersprungen werden. Das Eingabeargument R1 = 1 wird gesetzt.

data = csvread('daten1.csv', 1);

u_b = data(:, 1);
i_b = data(:, 2) * 1e-3;

---

In MATLAB 2019 wurde die readmatrix-Funktion integriert. Mit dieser können auch .xls- und .ods-Dateien in MATLAB eingelesen werden.

Download: daten1.ods

data = readmatrix('daten1.ods')

CSV-Dateien

Häufig werden für den Datenimport und -export CSV-Dateien verwendet:

• CSV: comma seperated values.
• Tabellen werden dargestellt durch Komma und Zeilenumbruch.

Beispiele der Datenauswertung

Einführung in die Regression mit polyfit

Aufgabe

Lesen Sie den Datensatz daten1.csv ein. Lassen Sie sich die Datenpunkten dieses Datensatzes graphisch darstellen.

Lösung

data = csvread('daten1.csv', 1);

u_b = data(:, 1);
i_b = data(:, 2) * 1e-3;

plot(u_b, i_b * 1e3, 'x');
grid('on')
xlabel('U_B / V');
ylabel('I_B / mA');

Regression mit polyfit

polyfit(x, y, n) führt eine Regression eines Polynom n-ten Grades der Datenpunkte \(y(x)\) durch.

Am Beispiel des Datensatzes:

• Regression eines Polynom zweiten Grades:

  >> poly = polyfit(u_b, i_b, 2)
  poly =
    -0.0096    0.0809    0.0003
  

• Resultierenden Funktion:

\[y(x) = -0.0096\cdot x^2 + 0.0809\cdot x + 0.0003\]

oder

\[I_B = -9.6\,\frac{\text{mA}}{\text V^2}\cdot {U_B}^2 + 80.9\,\frac{\text{mA}}{\text V}\cdot U_B+ 0.3\,\text{mA}\]

Darstellen der Regressionsfunktion

Mit Hilfe der polyval(poly, x) können Funktionswerte des Polynoms poly an der Stelle x berechnet werden.

>> polyval(poly, 0)
ans =
  272.7273e-006
>> polyval(poly, 4)
ans =
  170.2727e-003

Zur Darstellung der Regressionsfunktion, kann die Funktion elementweise durch polyval berechnet werden.

u_b2 = linspace(0, 4, 100);
i_b2 = polyval(poly, u_b2);

plot(u_b2, i_b2 * 1e3);

Lösung

Das gesamte Skript:

% Einlesen und Darstellen
%% Einlesen
data = csvread('daten1.csv', 1 );

u_b = data(:, 1);
i_b = data(:, 2) * 1e-3;

%% Plot
plot(u_b,i_b,'x')

grid('on')
xlabel('U_B / V');
ylabel('I_B / A');
hold('on')

%% Regression
poly = polyfit(u_b, i_b, 2);

%% Plotten der Regression
u_b2 = linspace(0, 4, 100);
i_b2 = polyval(poly, u_b2);

plot(u_b2, i_b2);
hold('off')

Analyse einer Wurfparabel

Der folgende Datensatz stammt aus einer Videoanalyse einer Wurfparabel. Ein Video des Basketballwurfs wurde aufgenommen und der Ball in den Einzelbildern markiert. Nach eine Kalibrierung der Distanzen im Video entsteht der Datensatz. Die Videoaufnahme fand mit 25 Bildern pro Sekunde statt.

Download: wurf1.csv

Aufgabe

Stellen Sie den Datensatz graphisch dar.
Führen Sie die Regression der Wurfparabel \(y(x)\) (quadratisches Polynom) durch.
Stellen Sie die Regressionsfunktion ebenfalls graphisch dar.

---

Für eine Wurfparabel gilt allgemein:

\[ y(x) = - \frac{g}{2 {v_0}^2 \cos^2 \alpha}x^2 + \tan \alpha \, x + h \]

mit Abwurfwinkel \(\alpha\), Abwurfgeschwindigkeit \(v_0\), Abwurfhöhe \(h\), Fallbeschleunigung \(g = 9{,}81\,\frac{\text m}{\text s^2}\).

Berechnen Sie aus den Koeffizienten der Regressionsfunktion \(\alpha, v_0, h\).

Wie kann die Genauigkeit der Koeffzientenbestimmung verbessert werden? Stichwort: Ballistische Kurve.

---

Welche anderen Möglichkeiten gibt es, die Werte \(\alpha, v_0, h\) zu berechnen.

Lösung

• Lösung:
  Parameter beim Erstellen der Wurfparabel::
  h = 2.4; v0 = 7.5; alpha = 55;

• Parameter aus den Koeffizienten der Wurfparabel:

  \[ y(x) = ax^2 + bx + c \]
  \[ h_0 = c \]
  \[ \tan \alpha = b \quad\rightarrow\quad \alpha = \arctan b \]
  \[ -\frac{g}{2{v_0}^2 \cos^2\alpha} = a \]
  \[\rightarrow \quad v_0^2 = -\frac{g}{2a\cos^2\alpha} \]
  \[\rightarrow \quad v_0 = \sqrt{-\frac{g}{2a\cos^2\alpha}} \]

• • $ h = y[0]$
  • Approximieren des Vektors der Anfangsgeschwindigkeit:

  Alterative Lösung:

  \[ \vec v_0 = \frac{\mathrm d}{\mathrm dt} \vec s |_{t=0} \approx \frac{\vec s[1] - \vec s[0]}{\Delta t} \]
  \[ v_{x,0} = \frac{x[1] - x[0]}{\Delta t} \]
  \[ v_{y,0} = \frac{y[1] - y[0]}{\Delta t} \]
  \[ \alpha = \arctan \frac{v_{y,0}}{v_{x,0}} \]
  \[ v_0 = \sqrt{{v_{x,0}}^2 + {v_{y,0}}^2} \]

clear, close all

%% Daten einlesen
data = csvread('wurf1.csv', 1);
% data = csvread('wurf2.csv', 1);
t = data(:, 1);
x = data(:, 2);
y = data(:, 3);

%% Graphiche Darstellung
plot(x, y, 'x')
grid on
xlabel('x / m')
ylabel('y / m')
axis('equal')
hold('on')

%% Regression
regend = length(x);
poly = polyfit(x(1:regend), y(1:regend), 4);
xreg = linspace(0, x(end));
yreg = polyval(poly, xreg);
plot(xreg, yreg);

%% Parameter aus den Koeffizienten der Wurfparabel
g = 9.81;
h = poly(3);
alpha = atand(poly(2));
v0 = sqrt(-g/(2*poly(1)*cosd(alpha)^2));

%% Parameter aus der Approximation der Anfangsgeschwindigkeit
vx0 = (x(2) - x(1))/(t(2)-t(1));
vy0 = (y(2) - y(1))/(t(2)-t(1)) + 0.5 * 9.81 * (t(2)-t(1));
v0_ = sqrt(vx0^2 + vy0^2);
alpha_ = atand(vy0/vx0);
hold('off')

Aufgabe

Passen Sie das Skript an, sodass auch der folgende Datensatz graphisch dargestellt und analysiert wird.

Download: wurf2.csv

Lösung

Parameter beim Erstellen der Wurfparabel:
h = 2; v0 = 5; alpha = 60;

Möglichkeiten der Kurvendiskussion mit Polynomen

roots(poly): Berechnen der Nullstellen eines Polynoms.
polyder(poly): Berechnen der Koeffizienten des Ableitungspolynoms.

Aufgabe

Berechnen Sie mit Hilfe der Regressionsfunktion des Datensatzes wurf1.csv die Wurfweite und Wurfhöhe.

Lösung

>> poly = polyfit(x, y, 2)
poly =
  -0.3952    1.5726    2.3410
>> roots(poly)
ans =
    5.6681e+000
    -1.2965e+000

Nullstellen:

\[x_{01} = 5.67\,\text m, \quad x_{02} = -1.30\,\text m\]

→ Wurfweite: \(5.67\,\text m\)

>> polyabl = polyder(poly)
polyabl =
  -0.7904    1.5726
>> xmax = roots(polyabl)
xmax =
    1.9895
>> polyval(poly, xmax)
ans =
    3.9054

Ableitungsfunktion:

\[ y(x) = -0.651 \,\frac{1}{\text m} x + 1.4231 \]

Extremstelle aus der Nullstelle der Ableitungsfunktion:

\[ x_E = 2.19\,\text m\]

Wurfhöhe aus dem Funktionswert an der Extremstelle

\[ y_{max} = f(x_E) = 3.91\,\text m \]

---

%% Nullstellen
Nst = roots(poly);
Nst = Nst(Nst > 0);
plot(Nst,zeros(size(Nst)),'o');

%% Hochpunkt
polyabl = polyder(poly);
xmax = roots(polyabl);
xmax = xmax(polyval(polyder(polyabl), xmax) < 0 & xmax > 0);
ymax = polyval(poly, xmax);
plot(xmax,ymax,'*b')

Entladen eines Kondensators

Aufgabe

Ein Kondensator wird über einem Widerstand \(R = 10\,\text k\Omega\) entladen. Die Anfangsspannung beträgt \(U_0 = 5\,\text V\).
Hierfür wurde die Kondensatorspannung \(u_C(t)\) mit einem Oszilloskop während des Entladevorgangs aufgezeichnet.
Es soll die Kapazität \(C\) des Kondensators bestimmt werden.

---

Der Entladevorgang des Kondensators über den Widerstand wurde mit Hilfe eines Oszilloskops aufgezeichnet. Ein Bildschirmfoto ist folgend zu sehen.

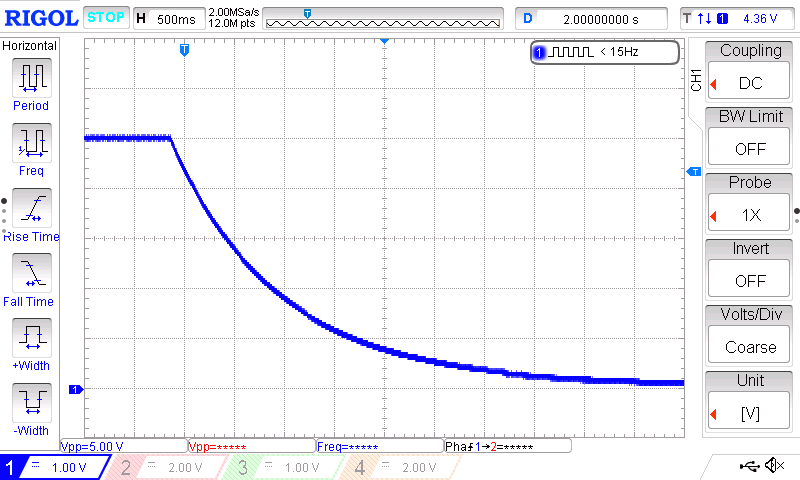
Außerdem wurde der folgende Datensatz aufgezeichnet: entladen1.csv

Aufbau des Datensatzes:

• 1. Spalte: Sample-Nummer.
  Abstand zwischen zwei Samples: \(5\,\text{ms}\).
• 2. Spalte: Kondensatorspannung in Volt.

---

Lesen Sie den Datensatz ein und stellen Sie diesen mit korrekter Achsenbeschriftung dar.
Bestimmen Sie eine sinnvolle Anfangs- und Endzeit des Ladevorgangs.
Approximieren Sie die Fläche unter der Kurve mit Hilfe der Rechteckregel.

Lösung

\[ C = \frac{Q_0}{U_0} \]

\[ Q_0 = \int_{t=0}^{\infty} i_C(t)\, \mathrm d t \]

\[ i_C(t) = \frac{u_C(t)}{R} \]

Es folgt:

\[ C = \frac{1}{U_0\cdot R} \int_{t=0}^\infty u_C(t)\,\mathrm d t\]

\[ \int_{t=t_1}^{t_2} u_C(t)\,\mathrm d t \approx \sum_{m=m_1}^{m_2} u_C[m] \cdot \Delta t \]

Lösung

%% Konstanten
dt = 5e-3;
U0 = 5;
R = 10e3;

%% Datensatz auslesen
data = csvread('entladen1.csv', 2);
t = data(:, 1) * dt;
uc = data(:, 2);

%% Plot
plot(t, uc);
grid('on')
xlabel('t / s')
ylabel('u_C / V')

%% Anfangs- und Endwert
tstart = 0.86;  % in sec
tend = 5;       % in sec

% Berechnung der Sample-Nummer
mstart = ceil(tstart / dt);
mend = ceil(tend / dt);

%% Integral
I = sum(uc(mstart:mend)) * dt;
C = 1/(U0 * R) * I

Aufgabe

Es wurde die Entlade-Funktion eines Kondensators mit einem anderen Kapazitätswert aufgezeichnet. Stellen Sie diese Funktion graphisch dar und bestimmen Sie den Kapazitätswert.

Download: entladen2.csv

---

Erweitern Sie das Skript, damit der Start- und Endzeitpunkt des Ladevorgangs automatisch bestimmt werden kann.

Lösung

\[C_1 \approx 100\,\mu\text F\]

\[C_1 \approx 47\,\mu\text F\]

Aufgabe

Stellen Sie die Ladefunktion in einem halblogarithmischen Plot mit Hilfe der semilogy-Funktion dar.

---

Implementieren Sie die Kapazitätsbestimmtung aus dem Datensatz entladen1.csv. mit Hilfe der Regressiongeraden. Stellen Sie die Funktion und die Regressionsgerade im halblogarithmischen Plot dar.

Lösung

Mathematischer Hintergrund:

\[ u_c(t) = U_0 \cdot e^{-\frac{t-t_0}{R\cdot C}} \]

\[ \ln \frac{u_c(t)}{U_0} = -\frac{t-t_0}{R\cdot C} \]

→ Lineare Funktion mit Anstieg:

\[ m = - \frac{1}{R \cdot C} \]

\[ C = - \frac{1}{m\cdot R} \]

Lösung

%% Konstanten
dt = 5e-3;
U0 = 5;
R = 10e3;

%% Datensatz auslesen
data = csvread('entladen1.csv', 2);
t = data(:, 1) * dt;
uc = data(:, 2);

%% Plot
semilogy(t, uc);
grid('on')
xlabel('t / s')
ylabel('u_C / V (log.)')
hold('on')

%% Anfangs- und Endwert
tstart = 0.86;  % in sec
tend = 5;       % in sec

% Berechnung der Sample-Nummer
mstart = ceil(tstart / dt);
mend = ceil(tend / dt);

%% Regression
poly = polyfit(t(mstart:mend), log(uc(mstart:mend)/U0), 1);
t_reg = linspace(tstart, tend, 10);
uc_reg = U0 * exp(polyval(poly, t_reg));
semilogy(t_reg, uc_reg);

%% Kapazitätsberechnung
C = -1/(poly(1)*R)
hold('off')