Einführung in die Systemanalyse mit MATLAB und Simulink

Systeme und Simulink

• Simulink ist ein MATLAB-Modul für die Simulation von technischen oder physikalischen Systemen.
• Was ist ein System?
  • Struktur, die Eingangssignale in Ausgangssignale umwandelt.
  • Besitzt meist einen internen Speicher (z. B. Integrator).
• Einfachste Form von Systemen: LTI-Systeme.
  • linear: Ist nur aus linearen Übertragungsgliedern aufgebaut
    (Addierer, Verstärker, Integratoren, Differentiatoren), alle Bauteilkennlinien sind linear.
  • zeit-invariant: Alle Bauteilparameter / Verstärkungsfaktoren bleiben während eines Versuches konstant.
    z. B. konstante Masse eines Federschwingers, konstante Kapazität eines Kondensators.

Beispiel

Leiten Sie die Differentialgleichung eines Feder-Masse-Dämpfer-Systems her. Wandeln Sie die Differentialgleichung in die Übertragungsfunktion um.

---

• Eingangsgröße: Externe Kraft \(F_E\).
• Ausgangsgröße: Position des Massestücks \(y\).

\[ m \ddot x + d \dot x + k x = F_E \]

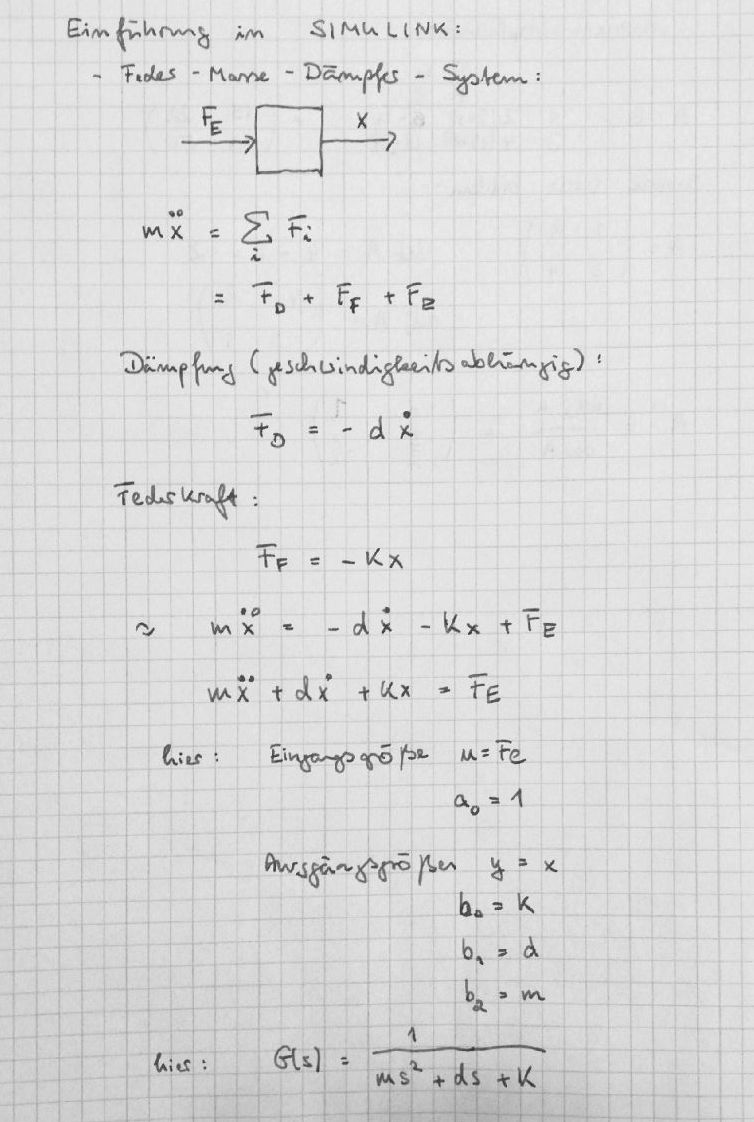
Differentialgleichung allgemein:

\[ b_m u^{(m)}(t) + \dots + b_1 \dot u(t) + b_0 u(t) = a_n y^{(n)}(t) + \dots + a_1 \dot y(t) + a_0 y(t)\]

Übertragungsfunktion allgemein:

\[ G(s) = \frac{b_m s^m + \dots + b_1 s + b_0}{a_n s^n + \dots + a_1 s + a_0} \]

\[ \rightarrow\quad G(s) = \frac{1}{m s^2 + d s + k} \]

MATLAB-Funktionen für die Systemanalyse

• Erstellen der Übertragungsfunktion mit der tf-Funktion:
  

  m = 1;
  d = .5;
  k = 10;
  
  sys = tf([1], [m, d, k]);
  

• Analyse des Systemsverhalten mit Hilfe der Polstellen der Übertragungsfunktion:
  

  >> pole(sys)
  ans =
    -250.0000e-003 +  3.1524e+000i
    -250.0000e-003 -  3.1524e+000i
  

  \(s_{P1,2} = -0.25 \pm 3.1524 i\)

  Mögliche Schlussfolgerungen:

  • Das System ist stabil: \(\text{Re}\{s_P\} > 0\).
  • Das System ist schwingungsfähig: \(\text{Im}\{s_P\} \neq 0\).

• Anzeige der Sprungantwort:
  Die Sprungantwort ist das Ausgangssignal des Systems, wenn der Eingang mit einem Sprung von 0 auf 1 belastete wird.
  

  step(sys)
  

• Anzeige der Impulsantwort:
  Antwort des Systems auf ein unendlich starken und kurzen Impuls.
  

  impulse(sys)
  

• Anzeige des Frequenzgang:
  Der Frequenzgang gibt an, wie stark das System mitschwingt, wenn ein Eingangssignal mit entsprechender Frequenz aufgeprägt wird.
  

  bode(sys)
  

Lösung

Interpretation:
- Bei kleinen Frequenzen schwingt das System gut mit.
- Bei großen Frequenzen kommt das System nicht mehr hinterher.
- Es gibt eine Resonanzfrequenz, bei der das Ausgangssignal um ca. 20 dB zunimmt
→ \(20\,\text{dB} \hat = 10\).

Systemanalyse mit Simulink

• Starten der Simulink-Umgebung mit dem simulink-Befehl.
• Erstellen eines neuen Modells.
• Das System muss in Simulink als Blockschaltbild aufgebaut werden.

Lösung

• Ein Blockschaltbild besteht in Allgemeinen aus aus folgenden Grundelementen:

  • Verstärker (Gain): \(x_A = k \cdot x_E\)
    Als Verstärkungsfaktor können Variablen aus dem Workspace verwendet werden: m, d, k.
  • Addierer (Sum): \(x_A = x_{E1} + x_{E2}\).
  • Integrator: $ x_A = \int x_E \,\mathrm d t + x_A(0)$.

• Die Differentialgleichung muss in die Integralform umgewandelt werden, um als Blockschaltbild dargestellt werden zu können.

\[ m \ddot x + d \dot x + k x = F_E \]

\[ \ddot x = \frac{1}{m}\left( F_E - (d \dot x + k x) \right) \]

• Aufbau:
  

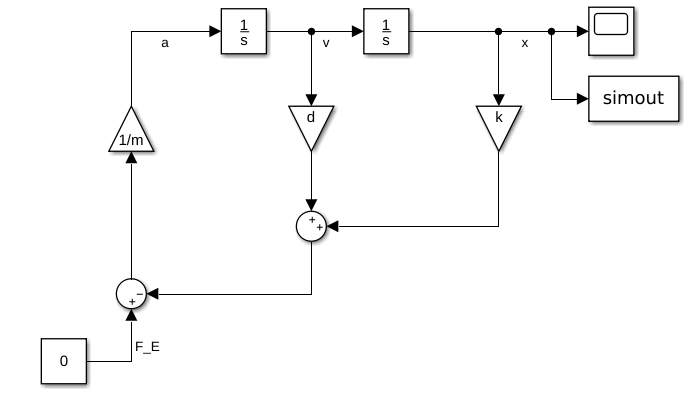
• Analyse der homogenen Lösung (Übergang des Systems in den energiefreien Zustand):
  • Verwenden der Konstante 0 als Eingangssignal.
  • Setzen der Anfangswerte der Intergratoren: \(v_0\), \(x_0\).
• Ausgangssignal kann mit dem Scope angezeigt werden.
• Alternativ wird die Variable simout in den MATLAB-Workspace exportiert:
  

  plot(simout)
  

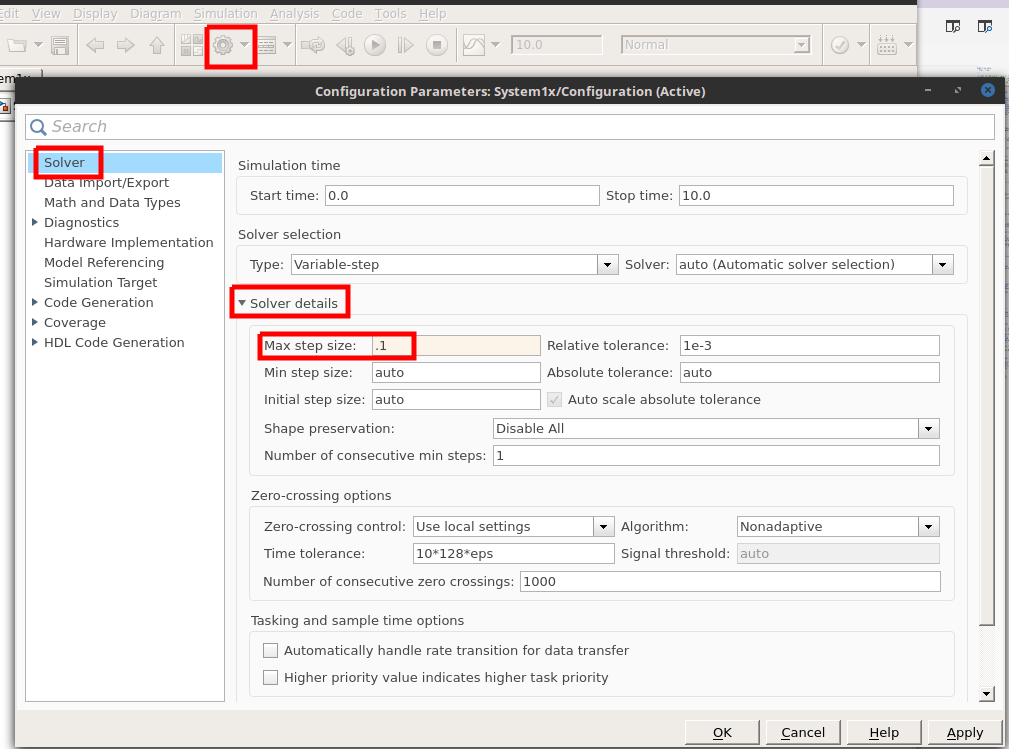
• Verringern der Schrittweite:
  Settings → Solver → Solver details → Max step size: 0.1
  

Aufgabe

Untersuchen Sie die Systemantwort bei verschiedenen Eingangssignalen.
Modellieren Sie die Systemantwort bei einer Sinus-Schwingung am Eingang. Wie verhält sich das System bei der Resonanzfrequenz?

Aufgabe

Leiten Sie die Differentialgleichung und die Übertragungsfunktion einen RC-Tiefpasses her.

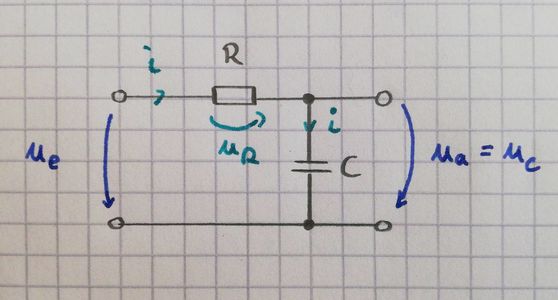
Lösung

• Eingangssignal: \(u_E\).
• Ausgangssignal: \(u_A = u_C\).

• Maschengleichung:

  \[ u_E = u_R + u_C \]

• Bauelementegleichungen:

  \[ u_R = R \cdot i \]
  \[ i = C \frac{\mathrm d}{\mathrm d t} u_C \]

• DGL:

  \[ u_E = R C\, \dot u_A + u_A \]

• Übertragungsfunktion:

  \[ G(s) = \frac{1}{R Cs + 1} \]

Aufgabe

Lassen Sie sich die Sprungantwort, Impulsantwort und Bode-Diagramm in MATLAB anzeigen.

Lösung

R = 10e3;
C = 10e-6;

sys = tf([1], [R*C, 1]);

step(sys)

Aufgabe

Bauen Sie das System in Simulink auf. Simulieren Sie den Entladenvorgang mit folgenden Bedingungen:

\[u_E(t) = 0, u_C(0) = 5\,\text V\]

Lösung

Umstellen der Differentialgleichung nach der höchsten Ableitung des Ausgangssignals:

\[ \dot u_A = \frac{1}{RC} \left( u_E - u_A \right) \]

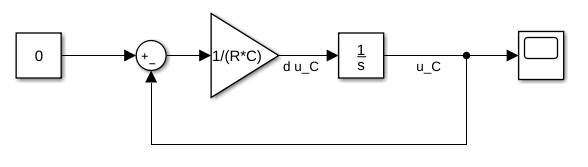
Aufgabe

Simulation bei einer Sinusschwingung variabler Frequenz am Eingang. Was zeichnet einen Tiefpassfilter aus?