Skripte und Funktionen

Workspace

Im Workspace sind alle globalen Variablen aufgelistet.
Alle Variablen gehen beim Programmneustart verloren!
Speichern der Variablen mit save-Anweisung möglich:
- save: Abspeichern aller Variablen in matlab.mat im akutellen Verzeichnis.
- save Dateiname: Spezifizieren des Dateinamens.
- save Dateiname x y: Nur ausgewählte Variablen werden abgespeichert.
  → Einfachste Möglichkeit Rechenergebnisse abzuspeichern.
Alternativ: Verwenden des Kontextmenüs des Workspace-Tabs.
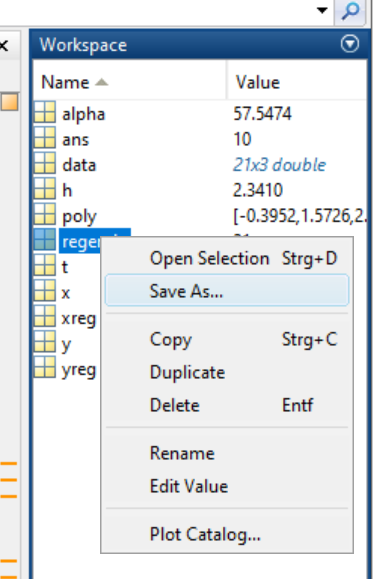
Laden von Variablen aus einer .mat-Datei erfolgt analog mit der load-Anweisung, alternativ über Open-Dialog.

Current Folder

Der Current Folder gibt das Arbeitsverzeichnis vor.
.mat oder .m-Dateien können in der Regel nur aus diesem Verzeichnis geladen werden.
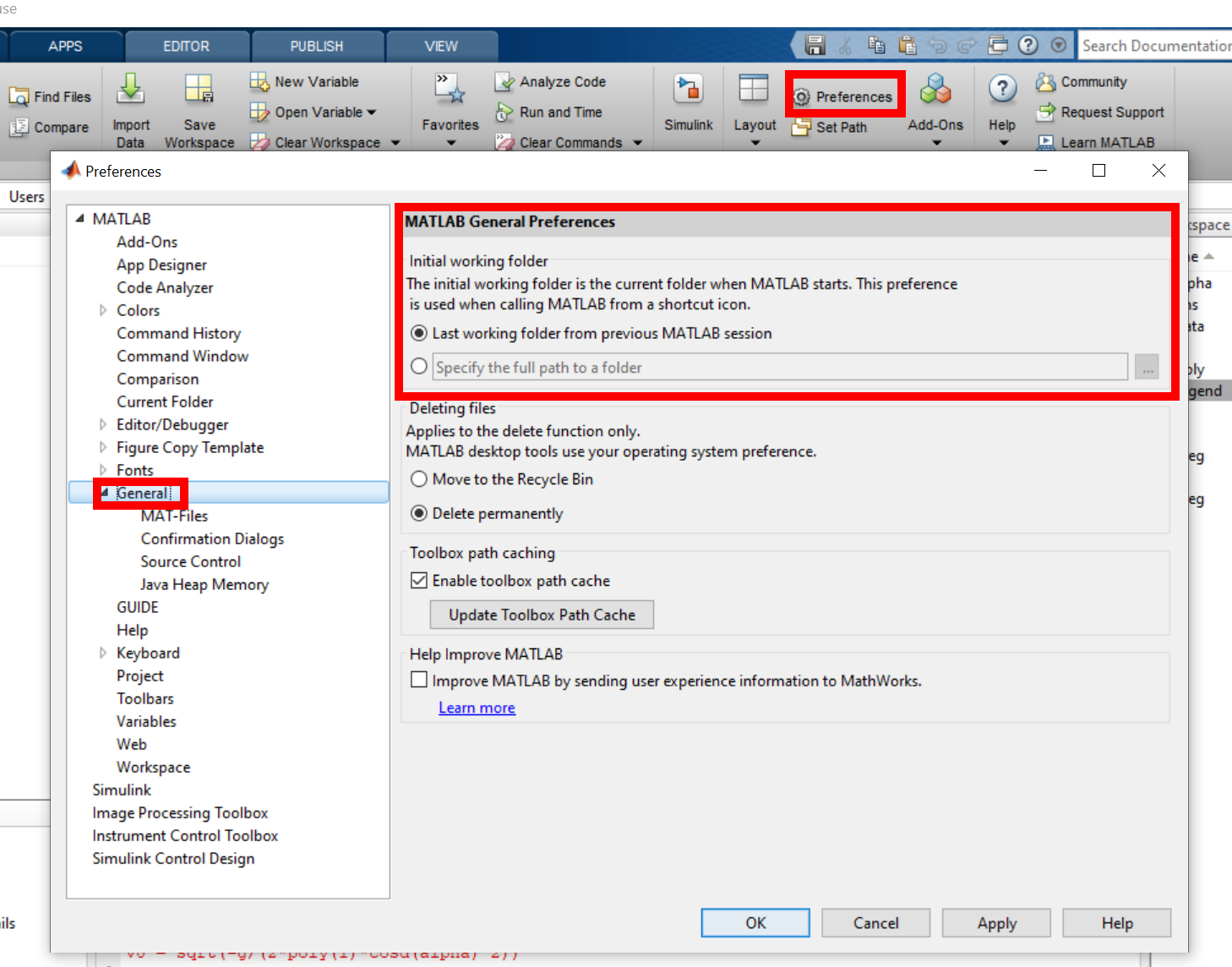
Current Folder kann durch Benutzeroberfläche oder durch die cd-Anweisung geändert werden.
Current Folder beim Start von MATLAB wird durch die Einstellung: General → Initial working folder festgelegt.

Skripte

Skripte werden als .m-Datei im Current Folder abgespeichert.
In Skripten wird eine Folge von Befehlen geschrieben, die sequentiell ausgeführt werden können.
Alle Operationen und Funktionen der Command-Window-Eingabe können verwendet werden.

Beispiel

Berechnen Sie den Widerstand einer \(100\,\text m\) langen Kupferleitung mit einen Leiterdurchmesser von \(1\,\text{mm}\).

Vorüberlegungen

\[ R = \frac{\rho\cdot l}{A} \]

\[ \rho_{Cu} = 1{,}8\cdot 10^{-8}\,\Omega\text m \]

\[ l = 100\,\text m\]

\[ A = \frac{\pi}{4}d^2\]

Erstellen eines neues Skriptes:

% Berechnung des Leitungswiderstands
%% Ausgangsgrößen
rho = 1.8e-8;   % spezifischer Widerstand in Ohm*m
l = 100;        % Länge in m
d = 1e-3;       % Durchmesser in m

%% Berechnung
A = pi/4*d^2;   % Berechnung der Querschnittsfläche
R = rho * l / A % Berechnung des Widerstandwertes in Ohm

Kommentare werden durch %-Zeichen gekennzeichnet.
- Kommentare können beliebigen Text enthalten, der nicht ausgeführt wird.
- z. B. Kurze Beschreibung des Skriptes in der ersten Zeile.
- oder ergänzende Informationen.
Auswahl des Dateinamens beim Speichern des Skriptes.
- entsprechend der MATLAB-Variablen-Konvention:
- nur Ziffern, Groß- und Kleinbuchstaben, Unterstrich.
- erstes Zeichen darf keine Ziffer sein.
- Um Konflikte mit eingebauten Funktionen zu vermeiden, sollten alle selbstgeschriebenen Funktionen mit einem Großbuchstaben beginnen.
  z. B. Widerstand1.m.
Ausführen über grünen Play-Button / F5.
Oder Eingabe des Skriptnamens im Command Window:
```
>> Widerstand1
R =
    2.2918
```
Alle Variablen der Skripte sind global (siehe Workspace).
Die Ausgabe von Rechenergebnissen erfolgt durch das Weglassen des Semikolon.
Durch %% wird ein neuer Abschnitt im Skript erstellt.
Abschnitte können mit Strg+Enter ausgeführt werden.

Aufgabe

Erstellen Sie ein Skript zur Berechnung der folgenden Aufgabe. Stellen Sie alle Größen und Zwischenergebnisse als Variablen dar.

Ein Kondensator \(C = 4{,}7\,\mu\text F\) wird über einen Widerstand \(R = 2{,}2\,\text k\Omega\) von einer Konstantspannungsquelle \(U_q = 5\,\text V\) geladen. Wie groß ist der Betrag der Kondensatorspannung \(u_C\) nach \(t = 20\,\text{ms}\)?

\[ u_C(t) = U_q\cdot (1-e^{-\frac{t}{\tau}}) \]

\[ \tau = R \cdot C \]

Lösung

% Berechnung der Kondensatorspannung beim Aufladevorgang

%% Eingangsgrößen
R = 2.2e3;     % in Ohm
C = 4.7e-6;    % in F
Uq = 5;        % in V
t = 20e-3;     % in s

%% Berechnung
tau = R*C;
uc = Uq * (1 - exp(-t/tau))

>> Claden
uc =
    4.2773

Aufgabe

Erstellen Sie ein Skript zur Berechnung der folgenden Aufgabe. Stellen Sie alle Größen und Zwischenergebnisse als Variablen dar.

Ein beidseitig eingespannter Balken mit einer Länge von \(l = 4\,\text m\) wird mit einer verteilten Streckenlast von \(q = 5\,\text{kN}/\text{m}\) belastet. Die Abmaße sind \(h=10\,\text{cm}\) und \(b=5\,\text{cm}\). Der Balken besteht aus Stahl und besitzt das E-Modul von \(E=21000\,\text{kN}/\text{cm}^2\). Berechnen Sie zunächst das Flächenträgheitsmoment \(I\) und anschließend die Durchbiegung in der Mitte.

\[ I = \frac{b \cdot h^3}{12} \]

\[ w_{Mitte} = \frac{q\cdot l^4}{384\cdot E\cdot I} \]

Lösung

%Berechnung der Durchbiegung von einem beidseitig eingespannten Balken

%% Eingangsgrößen
b=5;        %cm
h=10;       %cm
E=21000;    %kN/cm^2
l=400;      %cm
q=5e-2;     %kN/cm

%% Berechnung von Flächenträgheitsmoment
I=b*h^3/12; %cm^4

%% Berechnung der Durchbiegung
w=q*l^4/(384*E*I)   %cm

Funktionen

Funktionen werden in MATLAB ebenfalls in einer .m-Datei gespeichert.
Funktionen besitzen im Vergleich zu Skripten mehrere Eingabeparameter und mehrere Rückgabewerte.
Alle Variablen einer Funktion werden als lokal betrachtet.

Beispiel

Erstellen Sie eine Funktion für die Berechnung des Leitungswiderstandes aus spezifischem Widerstand, Leiterlänge und Leiterdurchmesser.

function [R] = Widerstand2(rho, l, d)
% WIDERSTAND2 Berechnung des Leitungswiderstands
%   R = WIDERSTAND2(rho, l, d) berechnet den Leitungswiderstand einer
%   Leitung mit spezifischen Widerstand rho, Länge l und Durchmesser d.

A = pi/4*d^2;
R = rho*l/A;
end

Der Name der Funktion muss mit dem Dateinamen übereinstimmen.
Eine kleine Beschreibung der Funktion kann eingefügt werden.
Aufrufen mit doc Widerstand2.
Beim Ausführen müssen die Parameter mit Werten versehen werden:
```
>> Widerstand2(1.8e-8, 100, 1e-3)
ans =
    2.2918
```

Lösung

Diskussion
- Objektorientierte Programmierung, Wiederverwendbarkeit
- Wann Funktion, wann Skript???

Lösung

A ist eine lokale Variable:

>> clear; Widerstand2(1.8e-8, 100, 1e-3);
>> whos A

Aufgabe

Erstellen Sie eine Funktion, die eine komplexe Zahl aus Betrag und Phase in Grad erstellt.

Eingabeparameter:
- Betrag: mag
- Phase in Grad: phase
Rückgabeparameter: komplexe Zahl z

Lösung

function [z] = Versor(mag, phase)
% VERSOR Erstellen einer komplexen Zahl mit dem Versoroperator
% z = VERSOR(mag, phase) erstellt eine komplexe Zahl aus Betrag und Phase
% in Grad
z = mag * exp(1i*deg2rad(phase));
end

>> Versor(2, 90)
ans =
  122.4647e-018 +  2.0000e+000i

Verwendung von 1i für die komplexe Einheit entsprechend der Warnung!

Aufgabe

Die Versor-Funktion soll für die Verwendung mit Matrizen umprogrammiert werden.
Eine mögliche Eingabe: Versor([1, 2], [90, 45])

Lösung

Alle Operationen müssen durch elementweise Operationen ersetzt werden.

function [z] = Versor(mag, phase)
% VERSOR Erstellen einer komplexen Zahl mit dem Versoroperator
% z = VERSOR(mag, phase) erstellt eine komplexe Zahl aus Betrag und Phase
% in Grad
z = mag .* exp(1i*deg2rad(phase));
end

>> Versor([1, 2], [90, 45])
ans =
  0.0000 + 1.0000i   1.4142 + 1.4142i

Aufgabe

Schreiben Sie eine Funktion, die den Betrag und die Phase in Grad einer komplexen Zahl ausgibt. Welche Möglichkeiten gibt es, mehrere Ausgabewerte auszugeben?

Lösung

Funktion mit zwei Ausgabewerten:

function [mag, phase] = CPolar(z)
% CPOLAR Ausgabe des Betrages und des Winkels eine komplexen Zahl
% CPOLAR(z)
mag = abs(z);
phase = rad2deg(angle(z));
end

>> CPolar(1+1i)
ans =
    1.4142
>> [m, p] = CPolar(1+1i)
m =
    1.4142
p =
    45

Nachteil: Funktion gibt standardmäßig nur den Betrag aus. Es muss nach beiden Werten gefragt werden.
Vorteil: Mit Werten kann weitergerechnet werden.

Funktion ohne Ausgabewerten:

function [] = CPolar(z)
% CPOLAR Ausgabe des Betrages und des Winkels eine komplexen Zahl
% CPOLAR(z)
mag = abs(z)
phase = rad2deg(angle(z))
end

>> CPolar(1+1i)
mag =
    1.4142
phase =
    45

Nachteil: Mit Werten kann nicht weitergerechnet werden.
Vorteil: Beide Werte werden von allein ausgegeben.

Ausgabe als Liste

function [result] = CPolar(z)
% CPOLAR Ausgabe des Betrages und des Winkels eine komplexen Zahl
% CPOLAR(z)
mag = abs(z);
phase = rad2deg(angle(z));
result = [mag, phase];
end

>> CPolar(1+1i)
ans =
    1.4142   45.0000

Verzweigungen

Bis jetzt: Funktionen und Skripte mit linearen Programmablauf.
Es folgt: Verzweigungen und Schleifen im Programmablauf.

If-Anweisung

Aufbau einer einfachen if-Anweisung:
```
if Bedingung
  Befehle...
end
```
Wenn die Bedingung wahr ist, dann werden die Befehle ausgeführt.
Bedingungen:
- Bedingungen können aus Vergleichsoperatoren und logischen Verknüpfungen bestehen.
- Vergleichsoperatoren:
  <: kleiner
  <=: kleiner gleich
  >: größer
  >=: größer gleich
  ==: gleich
  ~=: ungleich
- Logische Verknüpfungen:
  &: und
  |: oder
  ~: nicht

Beispiel

Schreiben Sie eine Funktion, die einen Eingabeparameter einen Wert auf 100 begrenzt.

\[ \text{Limit}(x) = \begin{cases} 100, & x > 100 \\ x, & \text{sonst} \end{cases} \]

function [x] = Limit(x)
if x > 100
    x = 100;
end
end

>> Limit(50)
ans =
    50
>> Limit(150)
ans =
  100

If-Anweisung mit Else-Anweisung

if Bedingung
  Befehle1...
else
  Befehle2...
end

Wenn die Bedingung wahr ist, dann werden die Befehle1 ausgeführt, ansonsten werden die Befehle2 ausgeführt.

Beispiel

Programmieren Sie die Signum-Funktion:

function [y] = Sign(x)
% SIGN Signum-Funktion
if x > 0
    y = 1;
else
    y = -1;
end
end

>> Sign(-4)
ans =
    -1
>> Sign(100)
ans =
    1

If-Anweisung mit Else-If-Anweisung

if Bedingung1
  Befehle1...
elseif Bedingung2
  Befehle2...
else
  Befehle3...
end

Wenn die Bedingung1 wahr ist, dann werden die Befehle1 ausgeführt, ansonsten wenn die Bedingung2 wahr ist, dann werden die Befehle2 ausgeführt.
Wenn keine der beiden Bedingungen wahr sind, werden die Befehle3 ausgeführt.

Beispiel

Erweitern Sie die Signum-Funktion, sodass nach der Definition ebenfalls gilt: \(\text{sgn}\,0 = 0\).

function [y] = Sign(x)
% SIGN Signum-Funktion
if x > 0
    y = 1;
elseif x < 0
    y = -1;
else
    y = 0;
end

>> Sign(0)
ans =
    0
>> Sign(-4)
ans =
    -1
>> Sign(100)
ans =
    1

Aufgabe

Programmieren Sie eine Clamp-Funktion, die die Eingangsvariable \(x\) zurückgibt, wenn diese innerhalb der angegebenen Grenzen \([a, b]\) liegt. Ansonsten wird die untere oder obere Grenze zurückgegeben.

\[ y = \text{Clamp}(x, a, b) = \begin{cases} x, & x \in [a, b] \\ a, & x < a \\ b, & x > b \end{cases}\]

Lösung

function [y] = Clamp(x, a, b)
% CLAMP Begrenzt die Eingangsvariable
% CLAMP(x, a, b) x wird im Intervall [a, b] begrenzt.
if x < a
    y = a;
elseif x > b
    y = b;
else
    y = x;
end
end

>> Clamp(-4, 0, 100)
ans =
    0
>> Clamp(72, 0, 100)
ans =
    72
>> Clamp(1e9, 0, 100)
ans =
  100

Switch-Anweisung

Motivation: Verwendung der switch-Anweisung, wenn eine if-Anweisung mit vielen Verzweigungen benötigt wird.

Zum Beispiel:

function [y] = Calc(a, b, op)
% CALC führt eine Berechnung mit zwei Operanden durch
if op == 1
    % Addition
    y = a + b;
elseif op == 2
    % Subtraktion
    y = a - b;
elseif op == 3
    % Multiplikation
    y = a .* b;
elseif op == 4
    % Division
    y = a ./ b;
elseif op == 5
    % Potenz
    y = a .^ b;
else
    % Fehler
    y = 0;
end
end

>> Calc(4, 5, 1)
ans =
    9
>> Calc(4, 5, 2)
ans =
    -1
>> Calc(4, 5, 3)
ans =
    20

→ Es werden verschiedene Werte einer Variable abgefragt und verschiedene Programmstücke ausgeführt.

Übersichtlicher und sicherer: Verwendung der switch-Anweisung

function [y] = Calc2(a, b, op)
% CALC2 führt eine Berechnung mit zwei Operanden durch
switch op
    case 1
        y = a + b;
    case 2
        y = a - b;
    case 3
        y = a .* b;
    case 4
        y = a ./ b;
    case 5
        y = a .^ b;
    otherwise
        y = 0;
end
end

Lösung

Weiteres Beispiel:
- op als optionaler Parameter.
- mehrere Eingabemöglichkeiten der Operationen:
Unterscheidung zwischen Zahlen und Zeichenketten

function [y] = Calc2(a, b, op)
% CALC2 führt eine Berechnung mit zwei Operanden durch

if nargin < 3
    op = 'add';
end

switch lower(op)
    case {1, 'add', '+', 'addieren'}
        y = a + b;
    case {2, 'sub', '-', 'subtrahieren'}
        y = a - b;
    case {3, 'mult', '*', 'multiplizieren'}
        y = a .* b;
    case {4, 'div', '/', 'dividieren'}
        y = a ./ b;
    case {5, 'pot', '^', 'potenzieren'}
        y = a .^ b;
    otherwise
        y = nan;
end
end

Schleifen

For-Schleife

Wichtigste Schleifen-Anweisung in MATLAB.
Aufbau:
```
for index = values
  statements
end
```
Der Schleifenrumpf statements wird hierbei für alle Elemente der Liste values ausgeführt.
statements werden length(values)-mal ausgeführt.
Die Variable index nimmt dabei jeweils einen Wert aus der Liste values an.

Beispiel

Geben Sie die Zahlen [1, 2, 4, 8] mit Hilfe der disp-Funktion aus.

for x = [1, 2, 4, 8]
  disp(x)
end

>>
  1
  2
  4
  8

Aufgabe

Programmieren Sie eine Funktion zur Berechnung des Fakultätswertes einer ganzen Zahl.

\[n! = \prod_{k=1}^n k\]

Lösung

function [y] = Factorial(n)
%FACTORIAL Berechnen der Fakultät
y = 1;
for k = 1:n
    y = y * k;
end
end

Aufgabe

Schreiben Sie eine Funktion, die die Summe aller ganzen Zahlen von 1 bis zum Eingabeparameter \(n\) berechnet.

\[\sum_{k=1}^n i\]

Lösung

function [y] = Sum(n)
% SUM berechnet aller ganzen Zahlen von 1 bis n
y = 0;
for k = 1:n
    y = y + k;
end

Aufgabe

Schreiben Sie eine Funktion, die die Summe der ersten \(n\) ungeraden Zahlen berechnet.

Lösung

\[ \sum_{k=1}^n (2k-1)\]

function [y] = Sum2(n)
% SUM berechnet der ersten n ungeraden Zahlen
y = 0;
for k = 1:n
    y = y + (2*k - 1);
end
end

Alternative Lösung:

function [y] = Sum2(n)
% SUM berechnet der ersten n ungeraden Zahlen
y = 0;
for k = 1:2:2*n
    y = y + k;
end
end

Lösung

In der Regel sollten alle geschriebenen Funktionen auf Vektoren anwendbar gemacht werden.

>> Sign([-4, 0, 10])
ans =
    0

→ Funktion kann nicht mit Vektoren verwendet werden!
- Vergleichsoperatoren können nur auf skalare Funktionen angewendet werden.
- Lösung: Mit Hilfe einer For-Schleife alle Elemente des Vektors einzeln berechnen.

Aufgabe

Schreiben Sie die Funktion Sign so um, dass diese elementweise auf einen Vektor angewendet werden kann. Verwenden Sie hierfür die for-Funktion, um den Vergleich auf jedes Element des Eingangsvektors einzeln anzuwenden.

Lösung

function [y] = Sign2(x)
% SIGN Signum-Funktion
for n = 1:length(x)
    if x(n) > 0
        y(n) = 1;
    elseif x(n) < 0
        y(n) = -1;
    else
        y(n) = 0;
    end 
end
end

>> Sign2([-4, 0, 10])
ans =
    -1     0     1
>> Sign2(10)
ans =
    1

Alternative Lösung mit Anhängen der Werte (y(end + 1)):

function [y] = Sign2(x)
% SIGN Signum-Funktion
y = [];
for xx = x
    if xx > 0
        y(end + 1) = 1;
    elseif xx < 0
        y(end + 1) = -1;
    else
        y(end + 1) = 0;
    end
end
end

arrayfun-Funktion

Alternativ kann mit der arrayfun-Funktion eine Funktion auf einen Vektor angewendet werden.

Beispiel im Command Window:

arrayfun(@(x) Sign(x), [-4 0 10])
ans =
    -1     0     1

Wie kann damit eine Funktion geschrieben werden?

function [y] = Sign3(x)
    y = arrayfun(@(x) Sign_(x), x);
end

function [y] = Sign_(x)
% SIGN Signum-Funktion
if x > 0
    y = 1;
elseif x < 0
    y = -1;
else
    y = 0;
end
end

Verwendung einer privaten Funktion Sign_.
Beim Aufrufen der Funktion Sign3 wird die arrayfun-Funktion elementweise angewendet.
Eine MATLAB .m-Datei kann mehrere Funktionen enthalten. Die Funktion,die dem Dateinamen entspricht, wird beim Aufrufen der Funktion ausgeführt. Alle andere Funktionen werden als private Funktionen angesehen. Auf diese Funktionen können von außen nicht zugegriffen werden.

Vorteile der arrayfun-Lösung
Form des Eingabevektors / der Eingabematrix bleibt erhalten:

>> Sign3([-4; 0; 10])
ans =
    -1
    0
    1

Lösung

Analyse der MATLAB-Implementation der sign-Funktion

Suche nach sign.m im MATLAB-Installationsordner:

function out = sign(in)
out = zeros(size(in));
out(in<0) = -1;
out(in>0) = +1;
end

Verwenden von Filteranweisungen:

>> a = [-4, 0, 10]
a =
    -4     0    10
>> a < 0
ans =
  1×3 logical array
  1   0   0
>> a(a<0)
ans =
    -4

While-Schleife

Der Rumpf(statements) einer While-Schleife wird wiederholt, solange eine Bedingung(expression) wahr ist.

while expression
  statements
end

Beispiel

Schreiben Sie ein Skript, das den Nutzer auffordert, eine positive Zahl einzugeben. Diese Eingabe soll wiederholt werden, wenn der Nutzer eine negative Zahl eingibt. Verwenden Sie für die Eingabe einer Zahl die input-Funktion.

n = -1;
while n < 0
    n = input('Positive Zahl: ');
end
disp(n)

>> PositiveInput
Positive Zahl: -3
Positive Zahl: -5
Positive Zahl: 7
    7

Aufgabe

Schreiben Sie ein Programm, dass die Quersumme einer natürlichen Zahl berechnet.

Tipps:

Modulo-Operator mod(a, b)
Gibt den Rest bei einer Ganzzahl-Division an.
```
mod(123, 10)
ans =
    3
```
mod(n, 10) liefert die letzte Stelle von n!
Mit floor(n / 10) kann die letzte Stelle von n entfernt werden.
```
>> floor(123 / 10)
ans =
    12
```

Lösung

Programmablaufplan:
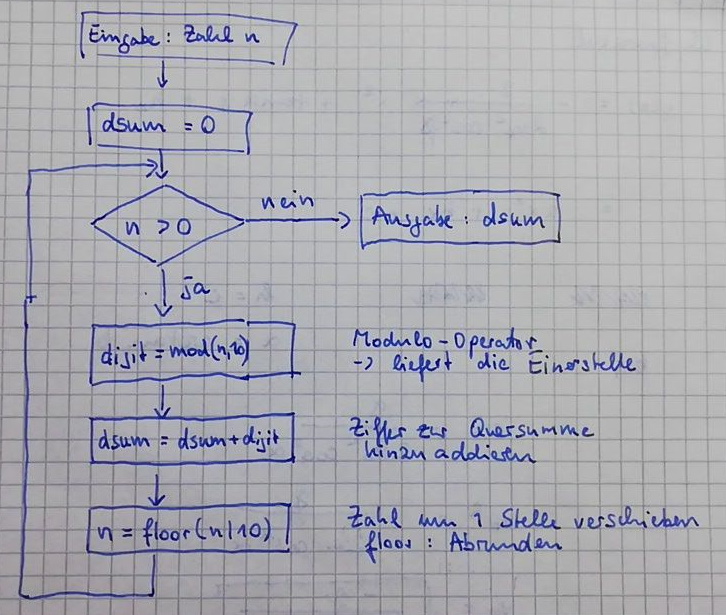
alt: "Programmablaufplan", w:50

function [dsum] = DigitSum(n)
%DIGITSUM Berechnen der Quersumme von n
dsum = 0;
while n > 0
    digit = mod(n, 10);
    dsum = dsum + digit;
    n = floor(n / 10);
end

Aufgabe

Schreiben Sie die Funktion aus der vorangegangenen Aufgabe um, sodass diese die Prüfziffer eine ISBN-10-Nummer berechnen kann.

Aufbau einer ISBN-10-Nummer am Beispiel von 0-7475-5100-6

Letzte Ziffer (6) ist die Prüfziffer.
Zur Berechnung der Prüfziffer werden die erste Ziffer mit 1, die zweite Ziffer mit 2, ..., die neunte Ziffer mit 9 multipliziert und alles aufaddiert.
Der Rest bei der Division dieser gewichteten Quersumme durch 11 ist die Prüfziffer. Ist die Prüfziffer 10, so wird ein X eingesetzt.

Am Beispiel:

>> 0*1 + 7*2 + 4*3 + 7*4 + 5*5 + 5*6 + 1*7 + 0*8 + 0*9
ans =
  116
>> mod(ans, 11)
ans =
    6

Die ISBN-Nummer soll wie folgt in die Funktion eingegeben werden: ISBN(074755100).

Lösung

Mit While-Schleife

function [pz] = ISBN(n)
%ISBN Berechnen der ISBN10-Prüfziffer
pz = 0;
w = 9;
while n > 0
    digit = mod(n, 10);
    pz = pz + digit * w;
    n = floor(n / 10);
    w = w - 1;
end
pz = mod(pz, 11);

Mit For-Schleife

function [pz] = ISBN(n)
%ISBN Berechnen der ISBN10-Prüfziffer
pz = 0;
for k = 1:9
    digit = mod(n, 10);
    pz = pz + digit * (10-k);
    n = floor(n / 10);
end
pz = mod(pz, 11);

Laufzeit-Analyse

Für größere Berechnung ist die Laufzeit einer Funktion entscheidend.
Es folgen Optimierungsansätze zum Verbessern der Laufzeit einer Funktion.
Beispiel für die Laufzeit-Analyse: Fibonacci-Folge.

\[y[k] = { 1, 1, 2, 3, 5, 8, ... }\]

\[y[k] = y[k-1] + y[k-2], \quad y[0] = y[1] = 1 \]

Aufgabe

Schreiben Sie eine Funktion Fibonacci(n), die rekursiv die ersten n Glieder der Fibonacci-Folge berechnet.

Lösung

function [y] = Fibonacci(n)
% FIBONACCI berechnet die ersten n Glieder der Fibonacci-Folge
for k = 1:n
    if k <= 2
        y(k) = 1;
    else
        y(k) = y(k-1) + y(k-2);
    end
end
end

>> Fibonacci(10)
ans =
    1     1     2     3     5     8    13    21    34    55

Aufgabe

Messen Sie die Laufzeit der Funktion Fibonacci mit Hilfe des tic- und toc-Befehls. Welcher Wert für n ist sinnvoll um ein reproduzierbares Ergebnis zu erhalten?

Lösung

>> tic;Fibonacci(1000);toc;
Elapsed time is 0.000619 seconds.

Mit \(n = 1000\) gibt es keine konstanten Ergebnisse
→ Laufzeitmessung ist stark abhängig von Hintergrundprozessen.
\(n = 10^6\) liefert konstante Ergebnisse, hier: \(t_L \approx 90\,\text{ms}\).

Deutliche Verbesserung der Laufzeit durch y = zeros(n); am Anfang des Programmes.

Aufgabe

Geben Sie mit Hilfe der disp-Funktion die Nummer des Gliedes aus, das aktuell berechnet wird. Wie verändert sich die Laufzeit? Wie kann die Anzahl der Ausgaben reduziert werden und der Fortschritt trotzdem angezeigt werden?

Lösung

Zeile 9: disp(k) einfügen → \(t_L \approx 40 \,\text{s}\).
Wenn Ausgaben benötigt werden, dann ist die Anzahl deutlich zu begrenzen!
```
if mod(k, 10000) == 0
    disp(k);
end
```
→ \(t_L \approx 140\,\text{ms}\)

Aufgabe

Implementieren Sie die Funktion Fibonacci mit Hilfe der expliziten Lösung der Fibonacci-Folge. Vergleichen Sie die Laufzeit!

\[ y[k] = \frac{f^k - (1-f)^k}{\sqrt{5}} \]

mit

\[ f = \frac{1+\sqrt{5}}{2} \]

Lösung

function [y] = Fibonacci2(n)
% FIBONACCI berechnet die ersten n Glieder der Fibonacci-Folge
f = (1 + sqrt(5)) / 2;
k = 1:n;
y = (f.^k - (1-f).^k) / sqrt(5);
end

\(t_L \approx 90\,\text{ms}\) → nicht langsamer als die rekursive Lösung.
→ Geschwindigkeitsgewinn, da eine Parallelisierung möglich ist.