Skip to content

Grundlagen

Eingabestruktur

  • Eingabeprompt >> zeigt an, dass eine Eingabe erwartet wird.
  • Eingabe durch Entertaste abschicken.

Lösung

>> 1+1
ans =
    2
>>
  • Variable ans (answer) speichert das letzte Rechenergebnis.
  • Unterdrücken der Ausgabe mit einem ; am Zeilenende.

Lösung

>> 1+2;
>>

Aufgabe

Welchen Wert nimmt ans an, wenn die Ausgabe einer Berechnung unterdrückt wurde?

Lösung

Die Ausgabe wird unterdrückt, jedoch wird die Variable ans trotzdem auf den Wert des letzten Rechenergebnisses gesetzt:

>> 1+1
ans =
    2
>> 1+2;
>> ans
ans =
    3
  • In der Regel kann in MATLAB nur 1 Befehl pro Zeile geschrieben werden. Mit , oder ; können mehrere Befehle einer Zeile getrennt werden.

Lösung

Durch das Semikolon wird die Ausgabe des ersten Befehls unterdrückt. Das Komma ermöglicht die Ausgabe des ersten und zweiten Befehls.

1+1;1+2
ans =
    3
>> 1+1,1+2
ans =
    2
ans =
    3
  • Trennen eines Befehls über mehrere Zeilen mit ....

Lösung

>> 1 ...
+1
ans =
    2

Ein Leerzeichen vor ... muss zwingend gesetzt werden!

Wichtige Konsolen-Befehle

Konsolen-Befehle

  • clear oder clear all
    Löschen aller Variablen des Workspaces.
  • clc
    Löschen des Command Windows.
  • help ... oder doc ... oder F1
    Zeigen der Hilfe / Dokumentation einer beliebigen Funktion.

Aufgabe

Schlagen Sie in der MATLAB-Hilfe nach, was die Befehlseingabe clear ans bewirkt. Testen Sie diesen Befehl.

Lösung

Es wird ledglich die Variable ans aus dem Workspace entfernt. Alle anderen Variablen bleiben erhalten.

Einstellen des Anzeigeformates

  • Die Ergebnisse einer Berechnung können in MATLAB auf verschiedene Arten dargestellt werden.
  • Es kann die Anzahl der Ziffern variiert werden (short, long).
  • Die Position des Kommas / Exponentialdarstellung kann variiert werden (normal, scientific, engineering).

  • Zwei Möglichkeiten der Einstellung:

    1. Über das Einstellungsmenü
      HOME → ENVIRONMENT → Perferences → MATLAB → Command Window → Text Display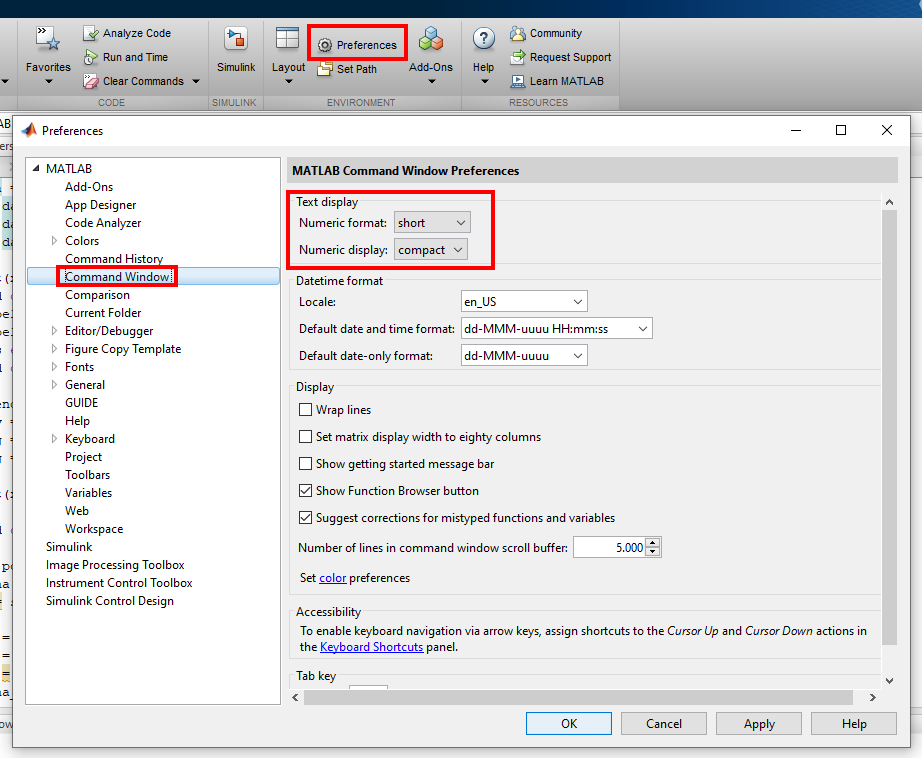

      alt: "Einstellen des Anzeigeformats", w:75

    2. Über den format-Befehl

      >> format shortEng
>> format compact

Aufgabe

Machen Sie sich mit den Einstellungsmöglichkeiten vertraut. Verwenden Sie die MATLAB-Dokumentation des format-Befehls.

Variablen

  • Variablen werden durch Wertzuweisung mit =-Operator erstellt.
    >> x = 5
  • Alle Variablen sind Matrizen. Deren Größe muss nicht festgelegt werden.

Lösung

>> whos x
  Name      Size            Bytes  Class     Attributes
  x         1x1                 8  double

Regeln der Variablenbenennung

  • Variablennamen müssen mit einen Buchstaben beginnen!
  • Zugelassen sind Buchstaben A-Z, a-z und Ziffern 0-9, Unterstrich _.
  • Keine Umlaute oder Sonderzeichen!
  • Es wird zwischen Groß- und Kleinschreibung unterschieden!
  • maximal 63 Zeichen.
  • Eingebaute Variablen von MATLAB werden überschrieben!!!
    z. B. pi, eps, inf, NaN

Lösung

>> pi = 3;
>> 2*pi
ans =
    6.0000
>> clear pi
>> 2*pi
ans =
    6.2832

Skalare Berechnungen

Eingabe von Zahlen

  • Dezimaldarstellung: Nachkommastellen zwingend mit Punkt . trennen.
    >> x = 1.5
>> x = .5
  • Exponentialdarstellung mit großem E oder kleinem e.
    >> x = 1.234e-15
>> x = 56.7E-5
>> x = 34.5e6

Mathematische Operationen

Mathematische Operationen"

  • +: Addition
  • -: Subtraktion
  • *: Multiplikation
  • /: Division
  • ^: Potenz
  • ( ): Klammern
    Es sind nur runde Klammern in mathematischen Berechnungen zulässig!

Beispiel

Berechnen Sie den ohmschen Widerstand \(R = \frac{U}{I}\) bei \(U = 5\,\text V\) und \(I = 1\,\text{mA}\).

>> U = 5; I = 1e-3; R = U/I
R =
    5000
>> format shortEng
>> U = 5; I = 1e-3; R = U/I
R =
    5.0000e+003

Aufgabe

Berechnen Sie die Spannung infolge einer Last von \(F=1\,\text{kN}\) auf eine Fläche von \(A=200\,\text{mm}^2\).

\[ \sigma = \frac{F}{A} \]

Das Ergebniss soll in \(\text N/\text{mm}^2\) oder in \(\text{kN}/\text{cm}^2\) angegeben werden.

Lösung

>> 1000/200
ans =
    5
>> 1/2
ans =
    0.5000
\[ \sigma = 5\,\text{N}/\text{mm}^2 = 0.5\,\text{kN}/\text{cm}^2 \]

Aufgabe

Dimensionieren Sie den elektrischen Kondensator:

\[ C = \frac{\varepsilon_0\cdot\varepsilon_r\cdot A}{d} \]

mit

\[\varepsilon_0 = 1{,}257\cdot 10^{-6}\,\frac{\text{As}}{\text{Vm}}, \varepsilon_r = 1, A = 10\,\text{mm}^2, d = 0{,}5 \,\text{mm}\]

Lösung

>> eps0 = 1.257e-6; epsR = 1; A = 10e-6; d = .5e-3; C = epsR*eps0*A/d
C =
  25.1400e-009
\[ C = 25{,}14\,\text{nF} \]

Mathematische Funktionen

  • MATLAB stellt viele mathematische Funktionen bereit.
  • Aufruf einer Funktion durch Angabe des Funktionsnamens und benötigten Parametern in runden Klammern:
    >> x = cos(0)
x =
    1
  • Auflistung aller Funktionen in MATLAB-Hilfe → Functions - By Category / Alphabetical List.

Überblick über mathematische Operationen

  • Trigonometrische Funktionen:
    sin(x): Sinus mit \(x\) in rad
    sind(x): Sinus mit \(x\) in Grad
    asin(x): Arcussinus mit \(x\) in rad
    asind(x): Arcussinus mit \(x\) in Grad
    cos(x), cosd(x), acos(x), acosd(x): Kosinus-Operationen
    tan(x), tand(x), atan(x), atand(x): Tangents-Operationen
    sinh(x), cosh(x), tanh(x), csc(x), sec(x), cot(x) : Weitere Winkelfunktionen
    deg2rad(x), rad2deg(x): Umrechnung zwischen Radian und Grad
  • Exponential-, Logarithmus und Wurzelfunktionen
    exp(x): Exponentialfunktion zur Basis e
    log(x): Logarithmus zur Basis e (ln)
    log10(x): Logarithmus zur Basis 10 (lg)
    log2(x): Logarithmus zur Basis 2 (ld)
    sqrt(x): Quadratwurzel (square root)
    nthroot(x, n): n-te Wurzel

Aufgabe

Die Katheten eines rechtwinkligen Dreiecks betragen \(5\,\text{cm}\) und \(6\,\text{cm}\). Wie lang ist die Hypotenuse? Wie groß sind drei Innenwinkel des Dreiecks?

Lösung

>> sqrt(5^2+6^2)
ans =
  7.810249675906654
>> atand(5/6)
ans =
  39.805571092265197
>> atand(6/5)
ans =
  50.194428907734810

Aufgabe

Ein Spannungverstärker liefert bei einer Eingangsamplitude von \(50\,\text{mV}\) eine Ausgangsamplitude von \(4\,\text{V}\). Welcher Verstärkung in Dezibel entspricht dies?

\[ v_U|_\text{dB} = 20 \,\text{dB} \cdot\lg(v_U) \]
\[ v_U = \frac{\widehat u_A}{\widehat u_E} \]

Lösung

>> vu = 4/50e-3
vu =
    80
>> vu_dB = 20*log10(vu)
vu_dB =
  38.061799739838868

Aufgabe

Wie wird die atan2/atan2d-Funktion verwendet? Wann sollte diese Funktion verwendet werden?

Lösung

Beispiel: Berechnen der Phase der komplexen Zahl \(z = -1 + j\), Erwartetes Ergebnis: \(135^\circ\)

\[\varphi = \frac{Im}{Re} = \frac{1}{-1} = -1\]
>> phi = atand(-1)
phi =
    -45
>> phi = atan2d(1, -1)
phi =
    135

Aufgabe

Wie bekommt man in MATLAB die Konstante e?

Lösung

>> exp(1)
ans =
  2.718281828459046

Vektoren

Allgemein

  • Definition eines Zeilenvektors:
    Eckige Klammern umschließen den Vektor, Trennen der Werte der Komponenten durch Leerzeichen oder Komma.
    >> v = [1 2 4 8]
>> v = [1, 2, 4, 8]
  • Zugriff auf die Elemente eines Zeilenvektors mit runden Klammern.
    >> v(3)
ans =
    4

    Die Indizierung von Vektoren und Matrizen beginnt in MATLAB im Gegensatz zu den meisten Programmiersprachen mit der 1!
    >> v(0)
Array indices must be positive integers or logical
values.
  • Verwendung des end-Operators: Zugriff auf das letzte und vorletzte Element des Vektors
    >> v(end)
ans =
    8
>> v(end - 1)
ans =
    4
  • Definition von Spaltenvektoren:
    Trennen der Werte der Komponenten durch Semikolon.
    w = [1; 2; 4; 8]

Funktionen zur Vektoranalyse

  • Apostroph-Zeichen v': Transponieren eines Vektors.
  • length(v): Größe eines Spalten- oder Zeilenvektors.

Lösung

>> w'
ans =
    1     2     4     8
>> v'
ans =
    1
    2
    4
    8
>> length(w)
ans =
    4
>> length(v)
ans =
    4

Doppelpunkt- oder Colon-Operator

  • n:m: Erstellen eines Zeilenvektors mit den Elementen n bis m:
    >> v = 1:5
v =
    1     2     3     4     5
  • n:k:m: Verwenden der Schrittweite k.
    >> v = 0:.2:1
v =
        0    0.2000    0.4000    0.6000    0.8000    1.0000
  • Der Colon-Operator kann zum Teilen von Listen verwendet werden:
    >> v(2:4)
ans =
    0.2000    0.4000    0.6000

Aufgabe

Erstellen Sie mit Hilfe des Colon-Operators eine Liste ungerade, die alle positiven ungeraden Zahlen kleiner als 100 enthält.

Lösung

>> ungerade = 1:2:100
ungerade =
  Columns 1 through 14
    1     3     5     7     9    11    13    15    17    19    21    23    25    27
  Columns 15 through 28
    29    31    33    35    37    39    41    43    45    47    49    51    53    55
  Columns 29 through 42
    57    59    61    63    65    67    69    71    73    75    77    79    81    83
  Columns 43 through 50
    85    87    89    91    93    95    97    99

Aufgabe

Erstellen Sie mit Hilfe des Colon-Operators die folgenden Listen:
10 9 8 7 6 5 4 3 2 1
10 8 6 4 2

Lösung

>> 10:-1:1
>> 10:-2:1

Aufgabe

Geben Sie die ersten 20 Elemente von ungerade an.
Geben Sie die jedes zweite Element von ungerade an (1, 5, 9, ...).

Lösung

>> ungerade(1:20)
ans =
  Columns 1 through 14
    1     3     5     7     9    11    13    15    17    19    21    23    25    27
  Columns 15 through 20
    29    31    33    35    37    39
>> length(ans)
ans =
    20
>> ungerade(1:2:length(ungerade))
ans =
  Columns 1 through 14
    1     5     9    13    17    21    25    29    33    37    41    45    49    53
  Columns 15 through 25
    57    61    65    69    73    77    81    85    89    93    97

Matrizen

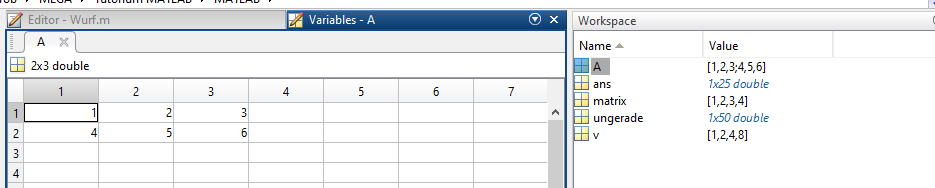
  • Definieren einer Matrix:
    Verwenden zum Kommas/Leerzeichen und Semikolons/Zeilenumbrüche.
    >> A = [1,2,3;4,5,6]
>> A = [1 2 3;4 5 6]
>> A = [1 2 3
4 5 6]

Oder: Eingabe einer Matrix über Workspace: New, Doppelklick.
alt: "Editieren oder Erstellen einer Matrix", w:75
- Zusammensetzen einer Matrix aus Vektoren:

>> A = [v; v]
>> B = [w, w]

Aufgabe

Welche Wirkung haben die Anweisungen A = [v, v] oder A = [w; w]?

Lösung

>> A = [v, v]
A =
    1     2     4     8     1     2     4     8

Mit diesen Befehlen können Listen zusammengefügt werden, oder Elemente an Listen angehangen werden.

Dies kann zum Anhängen von Werten an einen Vektor verwendet werden:

>> v = [v, 16]
v =
    1     2     4     8    16

Alternativer Weg mit end-Operator:

>> v(end + 1) = 32
v =
    1     2     4     8    16    32

Hinzufügen eines Elementes innerhalb der Liste

>> v = [v(1:2), 3, v(3:end)]
v =
    1     2     3     4     8
  • Zugriff auf Matrix-Elemente:
    • Zugriff auf ein Element:
      >> A(1,1)
ans =
    1
>> A(2,1)
ans =
    4
    • Eindimensionale Indizierung einer Matrix:
      >> A(1)
ans =
    1
>> A(4)
ans =
    5
    • Zugriff auf eine Matrix-Zeile:
      >> A(1,:)
ans =
    1     2     3
    • Zugriff auf eine Matrix-Spalte:
      >> A(:,1)
ans =
    1
    4

Funktionen zur Matrixanalyse

  • size(A): Größe einer Matrix
  • Apostroph ': Transponieren einer Matrix.
  • Funktionen zum automatischen Erstellen von Matrizen:
    ones(n, m): Matrix, deren Werte alle 1 betragen.
    zeros(n, m): Matrix, deren Werte alle 0 betragen.
    eye(n): Quadratische Einheitsmatrix.

  • Berechnungen:

    • Definition zweier Test-Matrizen:
      >> A = [1, 2; 3, 4]; B = [5, 6; 7, 8];
    • Addition und Subtraktion:
      >> A + B
ans =
  6     8
  10    12
>> A - B
ans =
  -4    -4
  -4    -4

    • Matrixmultiplikation:

      >> A * B
ans =
    19    22
    43    50
>> B * A
ans =
    23    34
    31    46

      Die Matrizenmultiplikation ist nicht kommutativ, das heißt, die Reihenfolge der Matrizen darf bei der Produktbildung nicht vertauscht werden.

    • Inverse einer Matrix:

      Für die Inverse \(A^{-1}\) der quadratischen \(n\times n\) Matrix \(A\) gilt:

      \[A\cdot A^{-1} = I\]

      \(I\) ist die \(n \times n\) Einheitsmatrix.

      Berechnung z. B. über die Adjunkte:

      \[A^{-1} = \frac{1}{\det A}\cdot\text{adj}\,A\]
      >> A^-1
ans =
  -2.0000    1.0000
    1.5000   -0.5000

Lösung

alt: "Berechnungen auf dem Papier", w:50

Beispiel

Lösen Sie das lineare Gleichungssystem:

\[ I\quad 5x + 3y = 31 \]
\[ II\quad 2x + y = 12 \]
\[ \begin{pmatrix} 5 & 3 \\ 2 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 31 \\ 12 \end{pmatrix}\]
\[A\cdot x = b\]
\[x = A^{-1} \cdot b\]
>> [5, 3; 2, 1]^-1 * [31; 12]
ans =
    5
    2

Aufgabe

Welche Bedeutung haben der /- und der \-Operator bei der Verwendung mit Matrizen?
Welche Berechnungen können mit dem \ einfacher dargestellt werden?

Lösung

A/B = A * B^-1
A\B = A^-1 * B

Lösung eines linearen Gleichungssystem: [5, 3; 2, 1] \ [31; 12]

Aufgabe

Berechnen Sie das Skalarprodukt von

\[\vec x = \begin{pmatrix} 5 \\ 3 \\ 1 \end{pmatrix} \]

und

\[\vec y = \begin{pmatrix} 7 \\ 1 \\ 0 \end{pmatrix} \]

Es gilt: \(<\vec x, \vec y> = \vec x^T \cdot \vec y\)

Lösung

>> [5;3;1]' * [7;1;0]
ans =
    38

Aufgabe

Lösen Sie das folgende Gleichungssystem mit den vier Unbekannten a, b, c, d.

\[ \begin{pmatrix} 6 & -1 & 1 & -12 \\ 6 & -2 & 2 & -8 \\ 3 & 0 & 2 & -4 \\ 3 & -1 & 0 & -4 \end{pmatrix} \cdot \begin{pmatrix} a \\ b \\ c \\ d \end{pmatrix} = \begin{pmatrix} -5 \\ 8 \\ 5 \\ 9 \end{pmatrix} \]

Lösung

>>  [6 -1 1 -12; 6 -2 2 -8; 3 0 2 -4; 3 -1 0 -4] \ [-5; 8; 5; 9]
ans =
    13
    6
    -5
    6

Aufgabe

Bestimmen Sie die Lösungsmenge der beiden folgenden Gleichungssysteme:

\[ \begin{pmatrix} 10 & 5 \\ -4 & -2 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 15 \\ 8 \end{pmatrix} \]
\[ \begin{pmatrix} 10 & 5 \\ -4 & -2 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 30 \\ -12 \end{pmatrix} \]

Lösung

>> [10 5; -4 -2] \ [15;8]
Warning: Matrix is singular to working precision. 

ans =
  -Inf
  Inf

→ Gleichungssystem mit leerer Lösungsmenge
\(\det A = 0\) → \(\frac{1}{\det A} = \infty\)

>> [10 5; -4 -2] \ [30;-12]
Warning: Matrix is singular to working precision. 

ans =
  NaN
  NaN

→ Gleichungssystem mit unendlich vielen Lösungen
\(\frac{0}{0} = \text{NaN}\), NaN = Not a Number

Ausgabe in älteren MATLAB-Versionen:

[10 5; -4 -2] \ [15;8]
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND =  1.110223e-17. 

ans =
  1.0e+17 *
  -0.6305
    1.2610

Beide Zahlen sind um 17 Größenordnungen größer als die Eingabewerte, also \(\approx \infty\)

>> [10 5; -4 -2] \ [30;-12]
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND =  1.110223e-17. 

ans =
    0
    6

Es wird eine mögliche Lösung des Gleichungssystems angegeben.

Aufgabe

Aufgabe aus dem bayrischen Abitur

Bei einer Losbude wird damit geworben, dass jedes Los gewinnt. Die Lose und die zugehörigen Sachpreise können drei Kategorien zugeordnet werden, die mit "Donau", "Main" und "Lech" bezeichnet werden. Im Lostopf befinden sich viermal so viele Lose der Kategorie "Main" wie Lose der Kategorie "Donau". Ein Los kostet 1 Euro. Die Inhaberin der Losbude bezahlt im Einkauf für einen Sachpreis der Kategorie "Donau" 8 Euro, in der Kategorie "Main" 2 Euro und in der Kategorie "Lech" 20 Cent. Ermitteln Sie, wie groß der Anteil der Lose der Kategorie "Donau" sein muss, wenn die Inhaberin im Mittel einen Gewinn von 35 Cent pro Los erzielen will.

Lösung

\[ D + M + L = 1 \]
\[ 4D = M \]
\[ -7D - M + 0{,}8L = 0{,}35 \]
>> [1 1 1; 4 -1 0; -7 -1 .8]\[1; 0; .35]
ans =
    0.0300
    0.1200
    0.8500

Aufgabe

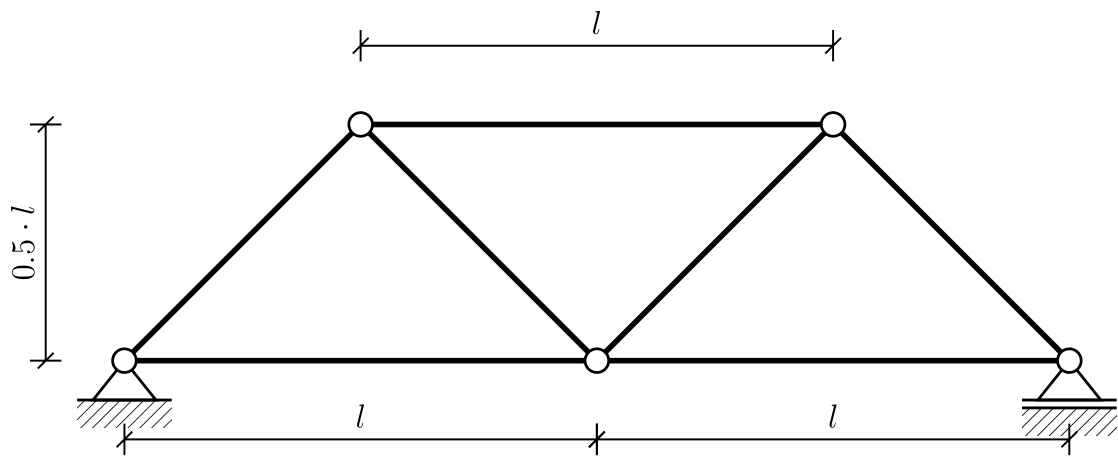
Berechnung der Verformung infolge äußerer Last

Folgende Struktur soll berechnet werden:

w: 50
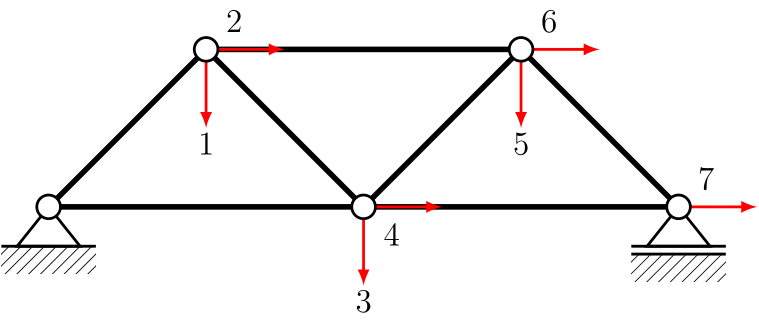
Definition der Freiheitsgrade und die zugehörige Flexibilitätsmatrix
w: 50
Die Strukturabhängige Eigenschaften sollen davor definiert werden: \(A=10\,\text{cm}^2\), \(E=210000\,\text{N}/\text{mm}^2\) und \(l=2.5\,\text{m}\). Die Steifigkeitsmatrix ist gegeben

K=E*A/l* ...
[sqrt(2)    0           -1/sqrt(2)  -1/sqrt(2)  0           0           0;
    0       1+sqrt(2)   -1/sqrt(2)  -1/sqrt(2)  0           -1          0;
-1/sqrt(2)  -1/sqrt(2)  sqrt(2)     0           -1/sqrt(2)  1/sqrt(2)   0;
-1/sqrt(2)  -1/sqrt(2)  0           2+sqrt(2)   1/sqrt(2)   -1/sqrt(2)  -1;
0           0           -1/sqrt(2)  1/sqrt(2)   sqrt(2)     0           -1/sqrt(2);
0           -1          1/sqrt(2)   -1/sqrt(2)  0           1+sqrt(2)   -1/sqrt(2);
0           0           0           -1          -1/sqrt(2)  -1/sqrt(2)  1+1/sqrt(2)];

Die Beziehung zwischen Belastung und Verschiebung ist folgendermaßen definiert

\[K \cdot x = f \]

Berechnen Sie die Verschiebung infolge einer Kraft von \(10\,\text{kN}\) an den Freiheitsgraden 3 und 5.

Lösung

  >> A=10; E=21000; l=250;
  >> K=E*A/l* ...
  [sqrt(2)    0           -1/sqrt(2)  -1/sqrt(2)  0           0           0;
    0       1+sqrt(2)   -1/sqrt(2)  -1/sqrt(2)  0           -1          0;
  -1/sqrt(2)  -1/sqrt(2)  sqrt(2)     0           -1/sqrt(2)  1/sqrt(2)   0;
  -1/sqrt(2)  -1/sqrt(2)  0           2+sqrt(2)   1/sqrt(2)   -1/sqrt(2)  -1;
  0           0           -1/sqrt(2)  1/sqrt(2)   sqrt(2)     0           -1/sqrt(2);
  0           -1          1/sqrt(2)   -1/sqrt(2)  0           1+sqrt(2)   -1/sqrt(2);
  0           0           0           -1          -1/sqrt(2)  -1/sqrt(2)  1+1/sqrt(2)];
  >> f=[0 0 10 0 10 0 0]';
  >> x=K\f

  x =

    0.0320
    0.0193
    0.0550
    0.0089
    0.0434
    0.0015
    0.0238

x in cm

Berechnungen von Messreihen

  • Größen einer Messreihe können als Vektor oder Matrix dargestellt werden.
  • In der Regel werden Rechenoperationen elementweise durchgeführt.
  • Addition, Subtraktion, Skalarmultiplikation können mit gewöhnlichen Operatoren +, -, * durchgeführt werden.

Lösung

>> A = [1, 2; 3, 4]; B = [5, 6; 7, 8];
>> A + B
ans =
    6     8
    10    12
>> A - B
ans =
    -4    -4
    -4    -4
>> 2 * A
ans =
    2     4
    6     8
  • Elementweise Multiplikation, Division und Potenzrechnung unterscheiden sich von den Matrixoperationen. Folgende Operatoren sind zu verwenden: .*, ./, .^

Lösung

>> A * B
ans =
    19    22
    43    50
>> A .* B
ans =
    5    12
    21    32

>> A^2
ans =
    7    10
    15    22
>> A.^2
ans =
    1     4
    9    16
  • Die elementaren mathematischen Funktionen können ebenfalls elementweise ausgeführt werden.

Lösung

>> sqrt(A)
ans =
    1.0000    1.4142
    1.7321    2.0000
>> x = 0:pi/2:4*pi
x =
        0    1.5708    3.1416    4.7124    6.2832    7.8540    9.4248   10.9956   12.5664
>> sin(x)
ans =
        0    1.0000    0.0000   -1.0000   -0.0000    1.0000    0.0000   -1.0000   -0.0000

Aufgabe

Wandeln Sie die folgenden Messreihe von Verstärkungfaktoren in Dezibel um.

\[ v_U|_\text{dB} = 20 \,\text{dB} \cdot\lg(v_U) \]
vu = [.1 .5 .707 1 1.4142 2 5 10 20 50 100];

Lösung

>> vu_dB = 20 * log10(vu)
vu_dB =
  Columns 1 through 10
  -20.0000   -6.0206   -3.0116         0    3.0102    6.0206   13.9794   20.0000   26.0206   33.9794
  Column 11
  40.0000

Aufgabe

Berechnen Sie den linearen Widerstand der Diodekennlinie.

\[ R = \frac{U}{I} \]
I = [.5 1 5 10 20 40 60 80 100] * 1e-3;
U = [.537 .573 .652 .683 .716 .749 .769 .782 .793];

Lösung

>> R = U./I
R =
    1.0740e+003   573.0000e+000   130.4000e+000    68.3000e+000    35.8000e+000    18.7250e+000    12.8167e+000     9.7750e+000     7.9300e+000

Möglichkeiten der Vektor- und Matrizenrechnung

Funktionen der Vektor- und Matrizenrechnung

  • norm(v): Betrag eines Vektors.
  • abs(v): Betrag der Vektorelemente
  • dot(u, v) oder u' * v: Skalarprodukt.
  • cross(u, v): Kreuzprodukt.
  • sum(v): Summe der Vektorelemente.
  • mean(v): Mittelwert der Vektorelemente.
  • max(v): Maximalwert der Vektorelemente.
  • min(v): Minimalwert der Vektorelemente.
  • prod(v): Produkt aller Vektorelemente

Aufgabe

Berechnen Sie den Winkel zwischen den Vektoren:

\[ \vec a = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \quad \vec b = \begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix} \]

Lösung

\[ \cos \varphi = \frac{<\vec a, \vec b>}{|\vec a|\cdot |\vec b|} \]
>> a = [1; 2; 3]; b = [2; 1; -3];
>> acosd(dot(a, b) / norm(a) / norm(b))
ans =
  110.9248

Aufgabe

Berechnen Sie die Fläche des Dreieckes, welches durch die folgenden drei Eckpunkt gegeben ist.

\[A(1, 0, 0)\]
\[B(0, 1, 2)\]
\[C(-1, 0, 3)\]

Lösung

\[ A_\Delta = \frac{1}{2} \left| \overrightarrow{AB} \times \overrightarrow{AC} \right| \]
>> A = [1; 0; 0]; B = [0; 1; 2]; C = [-1; 0; 3];
>> 1/2*norm(cross(B-A, C-A))
ans =
    1.8708

Aufgabe

Führen Sie eine Approximation des Mittelwerts \(\overline y\), Gleichrichtwerts \(\overline{|y|}\) und Effektivwert \(Y\) der Sinusschwingung \(y(t) = \sin t\) durch.

Verwenden Sie hierfür die folgende Sinusfolge:

>> t = 0:2*pi/100:2*pi;
>> y = sin(t);

Und die folgenden Approximationen:

  • Mittelwert:

    \[\overline y \approx \frac{1}{N} \sum_{i=1}^N y[i]\]

  • Gleichrichtwert:

    \[\overline{|y|} \approx \frac{1}{N}\sum_{i=1}^N \left| y[i] \right|\]

  • Effektivwert:

    \[ Y \approx \sqrt{\frac{1}{N} \sum_{i=1}^N \left( y[i] \right)^2} \]

Lösung

>> mw = mean(y)
mw =
  -3.9087e-17
>> grw = mean(abs(y))
grw =
    0.6302
>> ew = sqrt(mean(y.^2))
ew =
    0.7036

Beispiel

Schlagen Sie in der Dokumentation nach, wie die Funktionen min und max mit mehreren Ausgabewerten verwendet werden können. Bestimmen Sie die Extremstellen der Sinus-Funktion durch die zuvor verwendete Sinusreihe.

>> [ymax, nmax] = max(y)
ymax =
    1
nmax =
    26
>> t(nmax), pi/2
ans =
    1.5708
ans =
    1.5708
>> [ymin, nmin] = min(y)
ymin =
    -1
nmin =
    76
>> t(nmin), 3*pi/2
ans =
    4.7124
ans =
    4.7124

Funktionen der linearen Algebra

  • det(A): Determinante der Matrix.
  • eig(A): Eigenwerte der Matrix.

Aufgabe

Berechnen Sie die Determinante und Eigenwerte der folgenden Matrix:

\[ A = \begin{pmatrix} 4 & 5 & 3 \\ 3 & -1 & 1 \\ 0 & 3 & 1 \end{pmatrix} \]

Lösung

>> det([4 5 3; 3 -2 1; 0 3 1])
ans =
    -8
>> eig([4 5 3; 3 -2 1; 0 3 1])
ans =
    6.5020
    -3.8237
    0.3218

Aufgabe

Berechnen Sie die Eigenwerte der folgenden Matrix:

\[A = \begin{pmatrix} 2 & 1 \\ -1 & 2 \end{pmatrix}\]

Lösung

>> eig([2 1; -1 2])
ans =
  2.0000 + 1.0000i
  2.0000 - 1.0000i

→ konjugiert komplexes Paar Eigenwerte: \(\lambda_{1,2} = 2 \pm 1i\)

Komplexe Zahlen

  • Komplexe Zahlen werden in Matlab immer in der kartesischen Form (\(z = a + b\cdot i\)) abgespeichert.
  • Bei der Eingabe einer komplexen Zahl kann entweder i oder j als imaginäre Einheit verwendet werden.
  • Bei der Eingabe von komplexen Zahlen kann die imaginäre Einheit als Suffix verwendet werden:
>> 3 + 4i
ans =
  3.0000 + 4.0000i
>> 3 + 4*i
ans =
  3.0000 + 4.0000i
>> 3 + 4j
ans =
  3.0000 + 4.0000i
>> 3 + i4
Undefined function or variable 'i4'.
  • Viele Funktionen in MATLAB rechnen automatisch mit komplexen Zahlen:
    >> sqrt(-1)
ans =
  0.0000 + 1.0000i
  • Eingabe von komplexen Zahlen in der Polardarstellung ist vgl. aufwendig:
    >> 2 * exp(i * pi/4)
ans =
  1.4142 + 1.4142i
>> 2 * exp(i * deg2rad(45))
ans =
  1.4142 + 1.4142i

Funktionen zur Analyse komplexer Zahlen

  • abs(z): Betrag der komplexen Zahl.
  • angle(z): Phasenwinkel der komplexen Zahl.
  • conj(z) oder z': komplex konjugierte Zahl.
  • real(z): Realteil.
  • imag(z): Imaginärteil.

Aufgabe

Wandeln Sie die folgenden komplexen Zahlen zwischen der kartesichen und polaren Form um.

\[ z_1 = 3 + 4i\]
\[ z_2 = 5\cdot e^{i\cdot \pi/2} \]
\[ z_3 = 4 \angle 50^\circ \]

Lösung

>> z = 3+4i; abs(z), rad2deg(angle(z))
ans =
    5
ans =
  53.1301
>> 5*exp(i*pi/2)
ans =
  0.0000 + 5.0000i
>> 4*exp(i*deg2rad(50))
ans =
  2.5712 + 3.0642i

Aufgabe

Führen Sie die folgenden Berechnungen aus.

\[ (1+2i)\cdot(2-1i) = \]
\[ (5+7i)\cdot(5+7i)^* = \]
\[ \frac{4 \angle 50^\circ}{3-4i} = \]

Lösung

>> (1+2i)*(2-1i)
ans =
  4.0000 + 3.0000i
>> z = 5+7i; z*conj(z)
ans =
    74
>> 4*exp(i*deg2rad(50))/(3-4i)
ans =
  -0.1817 + 0.7791i

Aufgabe

Berechnen Sie den Strom \(i=i_1+i_2\) mit

\[ i_1 = 1\,\text A\cdot\sin(\omega t + 45^\circ),\]
\[ i_2 = 0{,}7\,\text A\cdot\sin(\omega t + 80^\circ),\]
\[ f = 50\,\text{Hz}.\]

Verwenden Sie die komplexe Tranformation:

\[\widehat I_1 = 1\,\text A \angle 45^\circ\]
\[\widehat I_2 = 0{,}7\,\text A \angle 80^\circ\]
\[ \widehat I = \widehat I_1 + \widehat I_2 \]

Lösung

>> i1 = exp(i*deg2rad(45));
>> i2 = 0.7*exp(i*deg2rad(80));
>> i = i1+i2
i =
  0.8287 + 1.3965i
>> abs(i), rad2deg(angle(i))
ans =
    1.6238
ans =
  59.3153
\[ i = 1{,}62\,\text A \cdot \sin(\omega t + 59{,}31^\circ) \]